|
|
ПРОБЛЕМЫ ФИЗИКИ, МАТЕМАТИКИ И ТЕХНИКИ №4 (49) 2021
ФИЗИКА
Князев М.А. Кинк модифицированного регуляризованного уравнения длинных волн
Аннотация. Рассмотрена новая версия модифицированного регуляризованного уравнения длинных волн. Уравнения такого типа используются в качестве альтернативы уравнению Кортевега-де Фриза. Модификация уравнения заключается в учете слагаемого, описывающего взаимодействие процессов дисперсии и диссипации. При помощи прямого метода Хироты решения нелинейных уравнений в частных производных построено решение типа кинка (антикинка) для модифицированного уравнения. Проанализирована возможность построения решения, описывающего связанное состояние кинка и антикинка.
Ключевые слова: регуляризованное уравнение длинных волн, кинк, антикинк, прямой метод Хироты.
Для цитирования: Князев, М.А. Кинк модифицированного регуляризованного уравнения длинных волн / М.А. Князев // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 7–10. – DOI: https://doi.org/10.54341/20778708_2021_4_49_7
Информация об авторах:
Князев Михаил Александрович – д.ф.-м.н., доцент, заведующий кафедрой инженерной математики Белорусского национального технического университета, Минск
Скачать PDF (201 КБ)
Коваленко Д.Л., Добромир М., Васькевич В.В., Семченко А.В., Сидский В.В.,
Тюленкова О.И., Косенок Я.А., Айвазян Г.Е., Лука Д. Разработка комбинированного метода
формирования ZnO / TiO2 нанотрубок
Аннотация. Определены условия формирования наноструктурных материалов на основе ZnO наностержней и формируемых на их основе TiO2 нанотрубок, оптимальные режимы нанесения и необходимая толщина затравочных ZnO
слоев. Экспериментальным путем подобраны временные и температурные режимы для гидротермального синтеза столбчатых наноструктур на основе оксида цинка. Методом атомно-силовой микроскопии проведены исследования морфологии и субшероховатости поверхности. С использованием растрового электронного микроскопа проведено
детальное изучение структуры и морфологии получаемых наноструктурированных материалов на каждом этапе
синтеза. Установлены основные характеристики, влияющие на размер и форму получаемых ZnO / TiO2 наноструктурных материалов.
Ключевые слова: гидротермальный метод, золь-гель метод, термообработка, ZnO наностержни, TiO2 нанотрубки, морфология поверхности, структурные свойства.
Для цитирования: Разработка комбинированного метода формирования ZnO / TiO2 нанотрубок / Д.Л. Коваленко, М. Добромир, В.В. Васькевич, А.В. Семченко, В.В. Сидский, О.И. Тюленкова Я.А. Косенок, Г.Е. Айвазян, Д. Лука // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 11–16. – DOI: https://doi.org/10.54341/20778708_2021_4_49_11
Информация об авторах:
Коваленко Дмитрий Леонидович – к.ф.-м.н., доцент, декан факультета физики и информационных технологий Гомельского государственно-го университета имени Франциска Скорины
Добромир Мариус – к.т.н., старший научный сотрудник института междисциплинарных исследований департамента точных и естественных наук Университета Александру Иоана Кузы, Яссы, Румыния
Васькевич Василий Васильевич – научный сотрудник НИСа, старший преподаватель кафедры радиофизики и электроники Гомельского государственного университета имени Франциска Скорины
Семченко Алина Валентиновна – к.ф.-м.н., доцент кафедры радиофизики и электроники Гомельского государственного университета имени Франциска Скорины
Сидский Виталий Валерьевич – к.т.н., доцент кафедры радиофизики и электроники Гомельского государственного университета имени Франциска Скорины
Тюленкова Ольга Ивановна – старший научный сотрудник НИСа Гомельского государственного университета имени Франциска Скорины
Косенок Янина Александровна – к.т.н., доцент кафедры оптики Гомельского государственного университета имени Франциска Скорины
Айвазян Гагик Ерджаникович – к.т.н., доцент института информационных и коммуникационных технологий Национального политехнического университета Армении, Ереван
Лука Дмитру – Университет Александру Иоана Кузы, Яссы, Румыния
Скачать PDF (1,73 MБ)
Можаровский В.В., Кузьменков Д.С., Коляскин И.И. Расчёт напряженно-деформированного состояния шины на примере её контакта с дорожным покрытием
Аннотация. Рассматривается задача приближённого расчёта напряженно-деформированного состояния изотропного основания (покрытия) на примере контакта шины и дорожного покрытия. Представлены основные зависимости для расчета напряженно-деформированного изотропного основания. На основе представленных формул разработан алгоритм решения исследуемой задачи и создана программа для расчёта напряженно-деформированного состояния массивной шины при контакте её с дорожным покрытием.
Ключевые слова: покрытие, шина колеса, напряженно-деформированное состояние, метод конечных элементов.
Для цитирования: Можаровский, В.В. Расчёт напряженно-деформированного состояния шины на примере её контакта с дорожным покрытием / В.В. Можаровский, Д.С. Кузьменков, И.И. Коляскин // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 17–20. – DOI: https://doi.org/10.54341/20778708_2021_4_49_17
Информация об авторах:
Можаровский Валентин Васильевич – д.т.н., профессор кафедры вычислительной математики и программирования Гомельского государственного университета имени Франциска Скорины
Кузьменков Дмитрий Сергеевич – к.ф.-м.н., доцент, заведующий кафедрой вычислительной математики и программирования Гомельского государственного университета имени Франциска Скорины
Коляскин Илья Игоревич – аспирант кафедры вычислительной математики и программирования Гомельского государственного университета имени Франциска Скорины
Скачать PDF (500 КБ)
Никитюк Ю.В., Сердюков А.Н., Аушев И.Ю. Оптимизация параметров лазерного раскалывания кварцевого стекла
Аннотация. Выполнена оптимизация параметров лазерного раскалывания кварцевых пластин. Оптимизационные расчеты проводились с использованием генетического алгоритма MOGA, реализованного в программе ANSYS.
Ключевые слова: лазерное раскалывание, кварцевая пластина, генетический алгоритм MOGA, программная система конечно-элементного анализа ANSYS.
Для цитирования: Никитюк, Ю.В. Оптимизация параметров лазерного раскалывания кварцевого стекла / Ю.В. Никитюк, А.Н. Сердюков, И.Ю. Аушев // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 21–28. – DOI: https://doi.org/10.54341/20778708_2021_4_49_21
Информация об авторах:
Никитюк Юрий Валерьевич – к.ф.-м.н., доцент, проректор по воспитательной работе Гомельского государственного университета имени Франциска Скорины
Сердюков Анатолий Николаевич – чл.-корр. НАН Беларуси, д.ф.-м.н., профессор кафедры оптики Гомельского государственного университета имени Франциска Скорины
Аушев Игорь Юрьевич – к.т.н., доцент, полковник внутренней службы, начальник факультета подготовки научных кадров университета гражданской защиты МЧС Республики Беларусь, Минск
Скачать PDF (1,54 MБ)
Пилипцов Д.Г. Влияние термообработки на механические свойства слоистых углеродных покрытий
Аннотация. Методами инструментального индентирования определено влияние режимов термообработки на механические свойства покрытий на основе углерода и композиционных нитридных слоев. Установлено увеличение твердости (Al-TiN) / а-С покрытия до 19,7 ГПа после отжига в вакууме при 400o С. Определены отношения H / E, H3 / E2,
характеризующие упругие свойства покрытий. Установлено увеличение стойкости к пластической деформации для покрытий, содержащих в своем составе алюминий после термообработки в вакууме. Анализ поведения коэффициентов упругого восстановления ηIT, полученных при разных глубинах индентирования, указывает на формирование более
однородной объёмной структуры и снижение градиента механических свойств по толщине в сравнении с неотожженными покрытиями.
Ключевые слова: углеродные покрытия, нитридные подслои, твердость, модуль упругости, наноиндентирование.
Для цитирования: Пилипцов, Д.Г. Влияние термообработки на механические свойства слоистых углеродных покрытий / Д.Г. Пилипцов // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 29–37. – DOI: https://doi.org/ 10.54341/20778708_2021_4_49_29
Информация об авторах:
Пилипцов Дмитрий Геннадьевич – к.т.н., доцент, ведущий научный сотрудник НИСа Гомельского государственного университета имени Франциска Скорины
Скачать PDF (666 КБ)
Руденков А.С. Морфология и фазовый состав наноструктурированных углеродных покрытий, cформированных на подслое, содержащем политетрафторэтилен и формиат свинца
Аннотация. Определены особенности морфологии, фазового состава углеродных покрытий, осажденных на подслои на основе политетрафторэтилена и формиата свинца различного состава. Установлено влияние массового соотношения компонентов исходной мишени, используемой для осаждения подслоя, и термообработки углеродных покрытий на их морфологию и фазовый состав. Оценена эффективность использования оксидов металлов и карбонизированных
полимерных слоев для заданного изменения фазового состава, рельефа углеродных покрытий.
Ключевые слова: углеродные покрытия, свинец, политетрафторэтилен, карбонизация, морфология, фазовый состав.
Для цитирования: Руденков, А.С. Морфология и фазовый состав наноструктурированных углеродных покрытий, формированных на подслое, содержащем политетрафторэтилен и формиат свинца / А.С. Руденков // Проблемы физики,
математики и техники. – 2021. – № 4 (49). – С. 38–44. – DOI: https://doi.org/10.54341/20778708_2021_4_49_38
Информация об авторах:
Руденков Александр Сергеевич – к.т.н., доцент, ведущий научный сотрудник НИСа Гомельского государственного университета имени Франциска Скорины
Скачать PDF (1,28 MБ)
Хахомов С.А., Семченко А.В., Сидский В.В., Васькевич В.В., Маевский А.А.,
Тюленкова О.И., Гайшун В.Е., Коваленко Д.Л., Пахомов О.В., Еськов А.В., Старков А.А.,
Холкин А.Л., Пилипенко В.А. Влияние состава и условий золь-гель процесса на свойства
сегнетоэлектрических тонких пленок титаната бария-стронция
Аннотация. Представлены результаты исследования влияния особенностей синтеза золь-гель методом, состава и
термообработки на микроструктуру, топографию поверхности и сегнетоэлектрические свойства тонких золь-гель
пленок BaxSr1-xTiO3 (x=0,8; 0,9; 1).
Ключевые слова: пленки BST, золь-гель метод, сегнетоэлектрики, гидролиз, поликонденсация, отжиг, сегнетоэлектрические свойства.
Для цитирования: Влияние состава и условий золь-гель процесса на свойства сегнетоэлектрических тонких пленок титаната бария-стронция / С.А. Хахомов, А.В. Семченко, В.В. Сидский, В.В. Васькевич, А.А. Маевский, О.И. Тюленкова, В.Е. Гайшун, Д.Л. Коваленко, О.В. Пахомов, А.В. Еськов, А.А. Старков, А.Л. Холкин, В.А. Пилипенко // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 45–50. – DOI: https://doi.org/10.54341/20778708_2021_4_49_45
Информация об авторах:
Хахомов Сергей Анатольевич – д.ф.-м.н., доцент, ректор Гомельского государственного университета имени Франциска Скорины
Семченко Алина Валентиновна – к.ф.-м.н., доцент кафедры радиофизики и электроники Гомельского государственного университета имени Франциска Скорины
Сидский Виталий Валерьевич – к.т.н., доцент кафедры радиофизики и электроники Гомельского государственного университета имени Франциска Скорины
Васькевич Василий Васильевич – научный сотрудник НИСа Гомельского государственного университета имени Франциска Скорины
Маевский Александр Артурович – магистр технических наук, младший научный сотрудник НИСа Гомельского государственного университета имени Франциска Скорины
Тюленкова Ольга Ивановна – старший научный сотрудник НИСа Гомельского государственного университета имени Франциска Скорины
Гайшун Владимир Евгеньевич – к.ф.-м.н., доцент кафедры оптики Гомельского государственного университета имени Франциска Скорины
Коваленко Дмитрий Леонидович – к.ф.-м.н., доцент, декан факультета физики и информационных технологий Гомельского государственного университета имени Франциска Скорины
Пахомов Олег Всеволодович – к.т.н., доцент, университет ИТМО, Санкт-Петербург
Еськов Андрей Владимирович – к.т.н., университет ИТМО, Санкт-Петербург
Старков Александр Сергеевич – к.ф.-м.н., доцент факультета систем управления и робототехники университета ИТМО, Санкт-Петербург
Холкин Андрей Леонидович – к.ф.-м.н., доцент, научный сотрудник университета ИТМО, Санкт-Петербург
Пилипенко Владимир Александрович – д.т.н., профессор, заместитель директора по научному развитию Государственного центра «Белмикроанализ» ОАО «ИНТЕГРАЛ», Минск
Скачать PDF (2,79 MБ)
Шилов А.В., Сотский А.Б. К достижению выраженной структурной окраски фотонно-кристаллического волокна
Аннотация. Определены условия получения выраженной структурной окраски фотонно-кристаллического волокна с гексагональной внутренней симметрией. Показано, что параметры волокна должны выбираться в соответствии с
конфигурацией запрещенных зон двумерного фотонного кристалла, сформированного заполняющими волокно воздушными каналами. Выводы зонной теории подтверждены расчетом поперечных сечений рассеяния фотонно-кристаллических волокон с круговой внешней границей.
Ключевые слова: структурная окраска, фотонно-кристаллическое волокно, зонная теория, поперечное сечение
рассеяния.
Для цитирования: Шилов, А.В. К достижению выраженной структурной окраски фотонно-кристаллического волокна / А.В. Шилов, А.Б. Сотский // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 51–56. – DOI: https://doi.org/10.54341/20778708_2021_4_49_51
Информация об авторах:
Шилов Артур Владимирович – старший преподаватель кафедры физики и информационных технологий Могилевского государственного университета им. А.А. Кулешова
Сотский Александр Борисович – д.ф.-м.н., профессор кафедры физики и информационных технологий Могилевского государственного университета им. А.А. Кулешова
Скачать PDF (613 КБ)
Юревич В.А. Нелинейное отражение сверхкороткого оптического импульса низкоразмерным суперкристаллом
Аннотация. Исследована динамика энергообмена низкоразмерной планарной решётки, образованной квантовыми
точками, с резонансным световым полем зондирующего извне импульса. В приближении однородного поля решена
задача описания коллективного эффекта сверхизлучения в рассматриваемом квазидвумерном суперкристалле (СК). Принципиальным в расчёте реакции СК является учёт диполь-дипольного взаимодействия активных центров в присутствии поглощения в квазирезонансных переходах – типичных для полупроводниковых СК механизмов нелинейности, вызывающих автомодуляционное смещение резонансной частоты поглощения (усиления).
Ключевые слова: суперкристаллы квантовых точек, диполь-дипольное взаимодействие, оптические коллективные эффекты, формализм вектора Блоха.
Для цитирования: Юревич, В.А. Нелинейное отражение сверхкороткого оптического импульса низкоразмерным
суперкристаллом / В.А. Юревич // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 57–63. – DOI: https://doi.org/10.54341/20778708_2021_4_49_57
Информация об авторах:
Юревич Владимир Антонович – д.ф.-м.н., доцент, профессор кафедры техносферной безопасности Белорусского государственного университета пищевых и химических технологий, Могилёв
Скачать PDF (502 КБ)
МАТЕМАТИКА
Бородич Р.В . О пересечении не
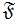 -подгрупп, выделяемых подгрупповым функтором,
в группах с операторами -подгрупп, выделяемых подгрупповым функтором,
в группах с операторами
Аннотация. Рассматривается строение подгруппы, связанной с пересечением ядер максимальных A-допустимых подгрупп, которые не содержат 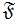 -корадикал и не принадлежат формации -корадикал и не принадлежат формации
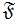 , индексы которых имеют ограничения.
Установлены свойства соответствующей обобщенной подгруппы Фраттини. , индексы которых имеют ограничения.
Установлены свойства соответствующей обобщенной подгруппы Фраттини.
Ключевые слова: конечная группа, формация,
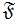 -корадикал. -корадикал.
Для цитирования:
Бородич, Р.В. О пересечении не 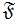 -подгрупп, выделяемых подгрупповым функтором, в группах
с операторами / Р.В. Бородич // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 64–68. – DOI: https://doi.org/10.54341/20778708_2021_4_49_64 -подгрупп, выделяемых подгрупповым функтором, в группах
с операторами / Р.В. Бородич // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 64–68. – DOI: https://doi.org/10.54341/20778708_2021_4_49_64
Информация об авторах:
Бородич Руслан Викторович – к.ф.-м.н., доцент, начальник НИСа Гомельского государственного университета имени Франциска Скорины
Скачать PDF (254 КБ)
Васильев А.Ф. О радикалах факторизуемых конечных 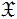 -групп -групп
Аннотация. Пусть
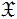 – насыщенная S-замкнутая формация конечных разрешимых групп, содержащая класс – насыщенная S-замкнутая формация конечных разрешимых групп, содержащая класс 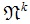 всех групп, нильпотентная длина которых не превосходит k, где k ≥ 3. В работе получено конструктивное описание всех формаций Фиттинга всех групп, нильпотентная длина которых не превосходит k, где k ≥ 3. В работе получено конструктивное описание всех формаций Фиттинга
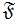 в в
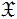 таких, что для любой таких, что для любой
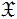 -группы G = AB выполняется -группы G = AB выполняется 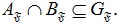
Ключевые слова: конечная группа, нильпотентная длина,
ди-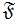 -группа, -группа,
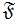 -радикал, формация Фиттинга, радикальная формация c условием Монахова в классе -радикал, формация Фиттинга, радикальная формация c условием Монахова в классе 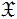 . .
Для цитирования: Васильев, А.Ф. О радикалах факторизуемых конечных 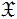 -групп / А.Ф. Васильев // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 69–75. – DOI: https://doi.org/10.54341/20778708_2021_4_49_69 -групп / А.Ф. Васильев // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 69–75. – DOI: https://doi.org/10.54341/20778708_2021_4_49_69
Информация об авторах:
Васильев Александр Фёдорович – д.ф.-м.н., доцент кафедры алгебры и геометрии Гомельского государственного университета имени Франциска Скорины
Скачать PDF (315 КБ)
Гальмак А.М. О порождающих множествах l-арной группы < Ak, [ ]l, σ, k >. III
Аннотация. В статье продолжается изучение связи между порождающими множествами группы A и порождающими множествами полиадической группы
< Ak, [ ]l, σ, k >
с l-арной операцией
[ ]l, σ, k, которая определяется на k-ой декартовой степени произвольной группы A для любого целого
l ≥ 2 и любой подстановки σ из множества
Sk всех подстановок множества {1, 2, …, k}.
Ключевые слова: группа, l-арная группа, порождающее множество.
Для цитирования: Гальмак, А.М. О порождающих множествах l-арной группы
< Ak, [ ]l, σ, k >. III / А.М. Гальмак // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 76–80. – DOI: https://doi.org/10.54341/20778708_2021_4_49_76
Информация об авторах:
Гальмак Александр Михайлович – д.ф.-м.н., профессор, заведующий кафедрой высшей математики Белорусского государственного университета пищевых и химических технологий, Могилёв
Скачать PDF (282 КБ)
Дергачева И.М., Шабалина И.П., Задорожнюк Е.А. Критерии 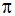 -отделимости конечной группы -отделимости конечной группы
Аннотация. В данной статье все группы конечны и G всегда обозначает конечную группу. Группа G называется
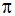 -отделимой, если каждый ее главный фактор является либо -отделимой, если каждый ее главный фактор является либо
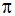 -группой, либо -группой, либо
 -группой. Подгруппа A группы G является -группой. Подгруппа A группы G является
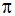 , ,  -субнормальной в G, если в G имеется цепь подгрупп -субнормальной в G, если в G имеется цепь подгрупп 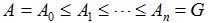 такая, что либо такая, что либо
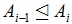 , либо , либо
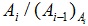 является является
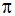 -отделимой группой для всех i = 1, …, n. В данной статье изучается влияние -отделимой группой для всех i = 1, …, n. В данной статье изучается влияние
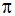 , ,  -субнормальных подгрупп на строение основной группы. -субнормальных подгрупп на строение основной группы.
Ключевые слова: конечная группа,
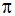 -отделимая группа, -отделимая группа,
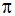 , ,  -субнормальная подгруппа, холлова подгруппа. -субнормальная подгруппа, холлова подгруппа.
Для цитирования: Дергачева, И.М. Критерии
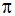 -отделимости конечной группы / И.М. Дергачева, И.П. Шабалина, Е.А. Задорожнюк // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 81–84. – DOI: https://doi.org/ 10.54341/20778708_2021_4_49_81 -отделимости конечной группы / И.М. Дергачева, И.П. Шабалина, Е.А. Задорожнюк // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 81–84. – DOI: https://doi.org/ 10.54341/20778708_2021_4_49_81
Информация об авторах:
Дергачева Ирина Михайловна – к.ф.-м.н., доцент, Белорусский государственный университет транспорта, Гомель
Шабалина Ирина Петровна – к.ф.-м.н., доцент кафедры высшей математики Белорусского государственного университета транспорта, Гомель
Задорожнюк Елена Андреевна – к.ф.-м.н., доцент, Белорусский государственный университет транспорта, Гомель
Скачать PDF (241 КБ)
Дудин А.Н., Синюгина Ю.В. Система поллинга с двумя марковскими входными потоками, конечными буферами и фазовым распределением времен обслуживания и переключения
Аннотация. Рассматривается система поллинга с двумя очередями с ограниченным числом мест в буферах. В каждую очередь поступает марковский поток требований. Времена обслуживания запросов и переключения между очередями распределены по фазовому закону. Дисциплина обслуживания очередей – шлюзовая. Получены формулы для нахождения стационарных вероятностей состояний системы в произвольный момент времени, а также формулы для вычисления основных характеристик производительности системы. Найдены выражения для преобразований Лапласа – Стилтьеса распределений времен ожидания в буферах.
Ключевые слова: система поллинга, марковский входной поток, фазовое обслуживание, стационарное распределение, время ожидания.
Для цитирования: Дудин, А.Н. Система поллинга с двумя марковскими входными потоками, конечными буферами и фазовым распределением времен обслуживания и переключения / А.Н. Дудин, Ю.В. Синюгина // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 85–91. – DOI: https://doi.org/10.54341/20778708_2021_4_49_85
Информация об авторах:
Дудин Александр Николаевич – д.ф.-м.н., профессор, заведующий лабораторией прикладного вероятностного анализа ФПМИ Белорусского государственного университета, Минск
Синюгина Юлия Васильевна – старший преподаватель кафедры фундаментальной и прикладной математики Гомельского государственного университета имени Франциска Скорины
Скачать PDF (282 КБ)
Казимиров Г.Н. Прямая и обратная теоремы теории приближений для обобщённого модуля гладкости некоторого класса функций
Аннотация. В статье доказывается совпадение обобщённых модулей гладкости k-го порядка, определяемых при помощи оператора обобщённого сдвига типа Гегенбауэра, с разными и одинаковыми сдвигами и как следствие получены прямая и обратная теоремы теории приближений алгебраическими многочленами.
Ключевые слова: наилучшее приближение алгебраическими многочленами, оператор обобщённого сдвига, обобщённый модуль гладкости.
Для цитирования: Казимиров, Г.Н. Прямая и обратная теоремы теории приближений для обобщённого модуля
гладкости некоторого класса функций / Г.Н. Казимиров // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 92–94. – DOI: https://doi.org/10.54341/20778708_2021_4_49_92
Информация об авторах:
Казимиров Григорий Николаевич – к.ф.-м.н., доцент кафедры математического анализа и дифференциальных уравнений Гомельского госу-дарственного университета имени Франциска Скорины
Скачать PDF (224 КБ)
Коновалова М.Н., Монахов В.С., Сохор И.Л. О строго 2-максимальных подгруппах конечных групп
Аннотация. Приводятся примеры конечных разрешимых и простых групп, в которых каждая 2-максимальная
подгруппа является строго 2-максимальной. Доказывается, что если в группе G существует строго 2-максимальная подгруппа порядка 2, то группа является сверхразрешимой группой порядка 2pq, где p и q – простые числа, не
обязательно различные, либо G изоморфна знакопеременной группе A4. Устанавливается строение конечной группы, в которой каждая 2-максимальная подгруппа является холловой. Для наследственной насыщенной решеточной формации 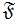 , содержащей все нильпотентные группы, и группы G ∉ , содержащей все нильпотентные группы, и группы G ∉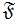 доказывается, что требование доказывается, что требование 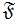 -субнормальности всех строго 2-максимальных подгрупп совпадает с требованием субнормальности всех 2-максимальных подгрупп. -субнормальности всех строго 2-максимальных подгрупп совпадает с требованием субнормальности всех 2-максимальных подгрупп.
Ключевые слова: конечная группа, 2-максимальная подгруппа, строго 2-максимальная подгруппа, холлова подгруппа, решеточная формация.
Для цитирования: Коновалова, М.Н. О строго 2-максимальных подгруппах конечных групп / М.Н. Коновалова, В.С. Монахов, И.Л. Сохор // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 95–100. – DOI: https://doi.org/10.54341/20778708_2021_4_49_95
Информация об авторах:
Коновалова Марина Николаевна – аспирантка Гомельского государственного университета имени Франциска Скорины, старший преподаватель кафедры социально-гуманитарных и естественнонаучных дисциплин Российской академии народного хозяйства и государственной службы при Президенте РФ, Брянск
Монахов Виктор Степанович – д.ф.-м. н., профессор кафедры алгебры и геометрии Гомельского государственного университета имени Франциска Скорины
Сохор Ирина Леонидовна – к.ф.-м.н., доцент кафедры прикладной математики и информатики Брестского государственного университета имени А.С. Пушкина
Скачать PDF (322 КБ)
Лось И.П., Сафонов В.Г. Об однопорожденных и ограниченных тотально ω-композиционных формациях конечных групп
Аннотация. Все рассматриваемые группы конечны. Пусть G – группа. Тогда через
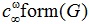 обозначают пересечение всех тотально ω-композиционных формаций, содержащих группу G. Формацию обозначают пересечение всех тотально ω-композиционных формаций, содержащих группу G. Формацию
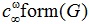 называют тотально
ω-композиционной формацией, порожденной группой G или однопорожденной тотально ω-композиционной формацией. Тотально ω-композиционная формация называют тотально
ω-композиционной формацией, порожденной группой G или однопорожденной тотально ω-композиционной формацией. Тотально ω-композиционная формация 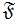 называется ограниченной, если она является подформацией некоторой
однопорожденной тотально ω-композиционной формации, т. е. называется ограниченной, если она является подформацией некоторой
однопорожденной тотально ω-композиционной формации, т. е.
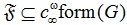 для некоторой группы G. В работе
получены критерии однопорожденности (ограниченности) тотально ω-композиционной формации. для некоторой группы G. В работе
получены критерии однопорожденности (ограниченности) тотально ω-композиционной формации.
Ключевые слова: формация конечных групп,
ω-композиционная формация, однопорожденная формация, ограниченная формация, тотально ω-композиционная формация.
Для цитирования: Лось, И.П. Об однопорожденных и ограниченных тотально ω-композиционных формациях конечных групп / И.П. Лось, В.Г. Сафонов // Проблемы физики, математики и техники. – 2021. – № 4 (49). – С. 101–107. – DOI: https://doi.org/10.54341/20778708_2021_4_49_101
Информация об авторах:
Лось Инна Павловна – младший научный сотрудник кафедры высшей алгебры и защиты информации Белорусского государственного университета, Минск
Сафонов Василий Григорьевич – д.ф.-м.н., профессор, проректор по научной работе Белорусского государственного университета, Минск
Скачать PDF (297 КБ)
|












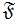 -подгрупп, выделяемых подгрупповым функтором,
в группах с операторами
-подгрупп, выделяемых подгрупповым функтором,
в группах с операторами
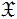 -групп
-групп
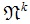 всех групп, нильпотентная длина которых не превосходит k, где k ≥ 3. В работе получено конструктивное описание всех формаций Фиттинга
всех групп, нильпотентная длина которых не превосходит k, где k ≥ 3. В работе получено конструктивное описание всех формаций Фиттинга
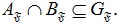
 -отделимости конечной группы
-отделимости конечной группы
 -группой. Подгруппа A группы G является
-группой. Подгруппа A группы G является
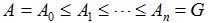 такая, что либо
такая, что либо
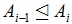 , либо
, либо
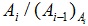 является
является
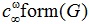 обозначают пересечение всех тотально ω-композиционных формаций, содержащих группу G. Формацию
обозначают пересечение всех тотально ω-композиционных формаций, содержащих группу G. Формацию
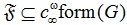 для некоторой группы G. В работе
получены критерии однопорожденности (ограниченности) тотально ω-композиционной формации.
для некоторой группы G. В работе
получены критерии однопорожденности (ограниченности) тотально ω-композиционной формации.