|
|
ПРОБЛЕМЫ ФИЗИКИ, МАТЕМАТИКИ И ТЕХНИКИ №2 (47) 2021
ФИЗИКА
Андреев В.В. Вычисление сечения каскадной реакции 2 → 4 методом базисных спиноров
Рассмотрена общая методика вычисления каскадных процессов в рамках улучшенного приближения узких резонансов. Учтены возможные экспериментальные ограничения на углы вылета конечных и промежуточных частиц. Важной отличительной чертой методики является использование пуанкаре-инвариантных спиральностей для конечных частиц каскадной реакции и метода базисных спиноров. В итоге сечение каскадного процесса ab → cd → 12 + 34 имеет компактную форму.
Ключевые слова: бинарная реакция, диаграмма Фейнмана, сечение, спиральность, парциальная ширина, распад.
Андреев Виктор Васильевич – доктор физ.-мат. наук, доцент, профессор кафедры теоретической физики факультета физики и информационных технологий Гомельского государственного университета имени Франциска Скорины
Скачать PDF (290 КБ)
Балмаков А.П., Слепенков Д.В., Хахомов С.А., Семченко И.В., Ванг Д., Cонг В. Создание с использованием 3D печати и фрезерования и экспериментальное исследование моделей метаповерхностей, покрывающих объекты сложной формы
В работе представлены результаты разработок, выполненных с использованием программ автоматизированного проектирования, аддитивных средств производства, таких как 3D принтеры, а также оборудования с числовым программным управлением. Изготовлены и экспериментально исследованы образцы метаповерхностей для экранизации металлических или металлизированных объектов сложной формы и уменьшения отражения излучения от них.
Ключевые слова: элементарная ячейка, элемент метаповерхности, омега элемент, электрическая проводимость, преобразование поляризации излучения, безэховая камера, коэффициент поглощения излучения.
Балмаков Алексей Петрович – кандидат физ.-мат. наук, доцент Гомельского государственного университета имени Франциска Скорины
Слепенков Дмитрий Владимирович – магистр естественных наук, аспирант Гомельского государственного университета имени Франциска Скорины
Хахомов Сергей Анатольевич – доктор физ.-мат. наук, ректор Гомельского государственного университета имени Франциска Скорины
Семченко Игорь Валентинович – доктор физ.-мат. наук, профессор, проректор по учебной работе Гомельского государственного университета имени Франциска Скорины
Джиченг Ванг – доцент, Университет Цзяннань, Уси
Вэй Сонг – кандидат физ.-мат. наук, доцент, Пекинский технологичсеский институт
Скачать PDF (2,54 МБ)
Бурый А.В., Ивашкевич А.В., Овсиюк Е.М., Редьков В.М. Структура плоских волн для поля со спином 2, массивный и безмассовый случаи
Изложена общая теория для поля со спином 2 на основе 30-компонентной системы уравнений первого порядка Федорова – Редже. В результате исключения в этих уравнениях дополнительных вектора и тензора третьего ранга выведены уравнения второго порядка Паули – Фирца для скаляра и симметричного тензора. Детально проанализирован предельный переход к безмассовому пределу; исследована имеющаяся согласно анализу Паули – Фирца калибровочная симметрия. В явном виде построены решения в виде плоских волн для массивной частицы, которые соответствуют пяти линейно независимым состояниям. В случае безмассового поля найдены 6 независимых решений и показано, что четыре из них являются калибровочными и, следовательно, могут быть исключены как нефизические. Два независимых решения, которые не содержат калибровочных степеней свободы, найдены в явном виде.
Ключевые слова: поле спина 2, уравнение второго порядка Паули – Фирца, уравнение первого порядка Федорова – Редже, плоские волны, независимые решения, безмассовая частица, устранение калибровочных степеней свободы.
Бурый Антон Васильевич – магистрант, стажер младшего научного сотрудника Центра «Фундаментальные взаимодействия и астрофизика» Института физики имени Б.И. Степанова Национальной академии наук Беларуси, Минск
Ивашкевич Алина Валентиновна – аспирант, младший научный сотрудник Центра «Фундаментальные взаимодействия и астрофизика» Института физики имени Б.И. Степанова Национальной академии наук Беларуси, Минск
Овсиюк Елена Михайловна – кандидат физ.-мат. наук, доцент, заведующая кафедрой теоретической физики и прикладной информатики Мозырского государственного педагогического университета имени И.П. Шамякина
Редьков Виктор Михайлович – доктор физ.-мат. наук, главный научный сотрудник Центра «Фундаментальные взаимодействия и астрофизика» Института физики имени Б.И. Степанова Национальной академии наук Беларуси, Минск
Скачать PDF (331 КБ)
Гришечкин Ю.А., Капшай В.Н. Некоторые решения дисперсионного уравнения для движущейся биизотропной среды
Получено дисперсионное уравнение для плоских монохроматических электромагнитных волн, распространяющихся в движущейся с постоянной скоростью биизотропной среде. В частных случаях распространения волны вдоль направления движения среды и противоположно ему найдены точные решения дисперсионного уравнения.
Ключевые слова: движущаяся биизотропная среда, материальные уравнения, уравнения Максвелла, показатель преломления, дисперсионное уравнение.
Гришечкин Юрий Алексеевич – кандидат физ.-мат. наук, доцент кафедры теоретической физики Гомельского государственного университета имени Франциска Скорины
Капшай Валерий Николаевич – кандидат физ.-мат. наук, доцент кафедры теоретической физики Гомельского государственного университета имени Франциска Скорины
Скачать PDF (243 КБ)
Малютина-Бронская В.В., Семченко А.В., Рогачёв А.В., Ярмоленко М.А., Сидский В.В., Данильченко К.Д., Сорока С.А., Русу Э.В. Фотоактивные свойства нанокомпозиционных покрытий ZnOx : MgО, осажденных в вакууме и методом золь-гель синтеза
Представлены результаты определения эффективности использования вакуумного осаждения и золь-гель синтеза при формировании нанокомпозиционных покрытий ZnOх : MgO с шириной запрещенной зоны большей 5 В и с высокой чувствительностью к УФ- и видимому излучению. Показано, что спектральная чувствительность гетероструктуры с шириной запрещенной зоны ZnOх : Mg порядка 6,2 эВ к УФ-излучению (278 нм) составила от 0,3 А / Вт до 3,23 А / Вт при смещении от 10 В до 14 В соответсвенно.
Ключевые слова: пленки ZnO : MgО, золь-гель метод, электронно-лучевое диспергирование, запрещенная зона, вольт-амперные характеристики, спектральная чувствительность.
Малютина-Бронская Виктория Владимировна – ГНПО «Оптика, оптоэлектроника и лазерная техника», Минск
Семченко Алина Валентиновна – кандидат физ.-мат. наук, доцент кафедры радиофизики и электроники Гомельского государственного университета имени Франциска Скорины
Рогачёв Александр Владимирович – доктор химических наук, профессор, член-корреспондент НАН Беларуси, директор Научно-исследовательского физико-химического института Гомельского государственного университета имени Франциска Скорины
Ярмоленко Максим Анатольевич – доктор технических наук, доцент кафедры радиофизики и электроники, ведущий научный сотрудник НИС Гомельского государственного университета имени Франциска Скорины
Сидский Виталий Валерьевич – кандидат технических наук, научный сотрудник НИСа Гомельского государственного университета имени Франциска Скорины
Данильченко Константин Дмитриевич – младший научный сотрудник кафедры оптикм Гомельского государственного университета имени Франциска Скорины
Сорока Сергей Александрович – ведущий инженер ГНПО «Оптика, оптоэлектроника и лазерная техника», Минск
Русу Эмил Васильевич – доктор технических наук, профессор, главный научный сотрудник лаборатории нанотехнологий Института электронной инженерии и нанотехнологий им. Д.В. Гицу АН Молдовы, Кишинев
Скачать PDF (591 КБ)
Рогачёв А.А., Лю Имин, Ярмоленко М.А., Гао Лихун, Ма Чжуа. Радиационная стойкость легированных металлами кремнийорганических покрытий, осаждаемых из газовой фазы
Определены молекулярная структура, морфология и радиационная стойкость кремнийорганических покрытий, легированных оксидами меди или вольфрама. Покрытия формировались из летучих продуктов электроннолучевого диспергирования механической смеси кремнийорганической смолы и соединений металлов. Показано, что медь- и вольфрамсодержащие кремнийорганические покрытия характеризуются значительно более низким содержанием метильных фрагментов. Влияние оксида вольфрама проявляется также в снижении содержания сшитых фрагментов в молекулярной структуре покрытия. Однокомпонентные и легированные металлами кремнийорганические слои являются высокодисперсными и бездефектными. Длительное воздействие УФ излучения не вызывает заметных изменений в их морфологии и молекулярной структуре.
Ключевые слова: нанокомпозиционные покрытия, кремнийорганические покрытия, ацетат меди, оксид вольфрама, электроннолучевое осаждение.
Рогачёв Александр Александрович – доктор технических наук, профессор, директор Института химии новых материалов Национальной Академии Наук Беларуси, Минск
Имин Лю – аспирант Гомельского государственного университета имени Франциска Скорины
Ярмоленко Максим Анатольевич – доктор технических наук, доцент кафедры радиофизики и электроники, ведущий научный сотрудник НИС Гомельского государственного университета имени Франциска Скорины
Лихун Гао – Пекинский технологический институт
Чжуа Ма – Пекинский технологический институт
Скачать PDF (671 КБ)
Руденков А.С., Пилипцов Д.Г., Ярмоленко М.А., Побияха А.С. Влияние режимов формирования на морфологию и фазовый состав углеродных покрытий, армированных многослойными углеродными нанотрубками
Рассмотрены морфологические особенности и фазовый состав углеродных покрытий, армированных углеродными нанотрубками и сформированных с различной частотой следования импульсов катодно-дугового источника углеродной плазмы. Показано, что армированные углеродные покрытия характеризуются большей субшероховатостью и перепадами рельефа (до 500 нм) по сравнению с неармированными нанотрубками покрытиями, что обусловлено присутствием агломератов МУНТ и их случайным распределением по поверхности. Установлено, что агломераты МУНТ вносят существенный вклад в формирование итогового КР-спектра, что, по всей видимости, обусловлено увеличением числа дефектов и аморфизацией стенок МУНТ в результате воздействия потока углеродной плазмы.
Ключевые слова: углеродные покрытия, углеродные нанотрубки, морфология, фазовый состав.
Руденков Александр Сергеевич – кандидат технических наук, доцент, ведущий научный сотрудник НИСа Гомельского государственного университета имени Франциска Скорины
Пилипцов Дмитрий Геннадьевич – кандидат технических наук, доцент, ведущий научный сотрудник НИСа Гомельского государственного университета имени Франциска Скорины
Ярмоленко Максим Анатольевич – доктор технических наук, доцент кафедры радиофизики и электроники, ведущий научный сотрудник НИС Гомельского государственного университета имени Франциска Скорины
Побияха Александр Сергеевич – старший преподаватель кафедры общей физики Гомельского государственного университета имени Франциска Скорины
Скачать PDF (1,29 МБ)
Старовойтов Э.И., Плескачевский Ю.М., Яровая А.В. Деформирование трехслойной круговой пластины в условиях ползучести
Аналитическое решение краевой задачи об осесимметричном изгибе круговой трехслойной пластины в условиях ползучести получено с помощью экспериментально-теоретического метода Ильюшина. Использованы физические уравнения состояния наследственной теории линейной вязкоупругости. Предполагалось подобие ядер ползучести материалов слоев. Для описания кинематики несимметричного по толщине пакета пластины принята гипотеза ломаной линии. В несущих слоях справедливы гипотезы Кирхгофа. В относительно толстом заполнителе принята гипотеза Тимошенко. В качестве исходного взято известное решение аналогичной задачи теории упругости для подобной трехслойной пластины. Проведена численная апробация полученного решения.
Ключевые слова: трехслойная пластина, изгиб, подобие ядер ползучести, экспериментально-теоретический метод.
Старовойтов Эдуард Иванович – доктор физ.-мат. наук, профессор, зав. кафедрой «Строительная механика» Белорусского государственного университета транспорта, Гомель
Плескачевский Юрий Михайлович – член.-корр. НАН Беларуси, д.т.н., профессор, зав. кафедрой «Микро- и нанотехника» Белорусского национального технического университета, Минск
Яровая Анна Владимировна – доктор физ.-мат. наук, профессор, профессор кафедры «Строительная механика» Белорусского государственного университета транспорта, Гомель
Скачать PDF (405 КБ)
Шалупаев С.В., Никитюк Ю.В., Середа А.А., Аушев И.Ю. Моделирование процесса
разделения многослойных неоднородных структур из стекла по криволинейным контурам
В рамках теории термоупругости выполнен сравнительный анализ полей термоупругих напряжений, возникающих в многослойных структурах из стекла (триплекс) в процессе двулучевого управляемого лазерного термораскалывания. При этом вдоль линии обработки предварительно наносится серия каналов перпендикулярных поверхности материала. Показано, что при наличии каналов величина максимальных растягивающих напряжений существенно увеличивается и зависит от радиуса каналов, расстояния между ними и параметров обработки. Серия нанесенных каналов вдоль линии обработки позволяет контролировать инициализацию и развитие трещины вдоль линии обработки по криволинейным траекториям.
Ключевые слова: термораскалывание, моделирование, метод конечных элементов, температура, триплекс, термоупругие напряжения.
Шалупаев Сергей Викентьевич – кандидат физико-математических наук, доцент кафедры общей физики Гомельского государственного университета имени Франциска Скорины
Никитюк Юрий Валерьевич – кандидат физико-математических наук, доцент, проректор по воспитательной работе Гомельского государственного университета имени Франциска Скорины
Середа Андрей Александрович – старший преподаватель кафедры радиофизики и электроники Гомельского государственного университета имени Франциска Скорины
Аушев Игорь Юрьевич – кандидат технических наук, доцент, полковник внутренней службы, начальник факультета подготовки научных кадров Университета гражданской защиты МЧС Республики Беларусь, Минск
Скачать PDF (305 КБ)
МАТЕМАТИКА
Гальмак А.М. О порождающих множествах l-арной группы < Ak, [ ]l, σ, k >. I
Устанавливается связь между порождающими множествами группы А и порождающими множествами полиадической группы < Ak, [ ]l, σ, k > с l -арной операцией [ ]l, σ, k, которая определяется на k-ой декартовой степени произвольной группы А для любого целого l ≥ 2 и любой подстановки σ из множества Sk всех подстановок множества {1, 2, …, k}.
Ключевые слова: группа, l-арная группа, порождающее множество.
Гальмак Александр Михайлович – доктор физ.-мат. наук, доцент, заведующий кафедрой высшей математики Белорусского государственного университета пищевых и химических технологий, Могилёв
Скачать PDF (348 КБ)
Жогаль С.П., Жогаль С.И., Орлов В.В. Исследование влияния случайных возмущений на колебания в сложных квазилинейных системах с запаздыванием
Исследованы вопросы воздействия случайных сил на колебательные процессы в системах, описываемых дифференциальными уравнениями, содержащих как звенья с сосредоточенными параметрами, так и звенья с распределенными параметрами и запаздыванием, связанные между собой запаздывающими связями. Описывается поэтапное применение метода усреднения нелинейной механики и метода уравнений Фоккера – Планка – Колмогорова к исследованию таких систем.
Ключевые слова: стохастические дифференциальные уравнения, запаздывание, стохастические дифференциальные уравнения в частных производных, звенья с сосредоточенными параметрами, звенья с распределенными параметрами, метод усреднения нелинейной механики, метод уравнений Фоккера – Планка – Колмогорова.
Жогаль Сергей Петрович – кандидат физ.-мат. наук, доцент, декан факультета математики и технологий программирования Гомельского государственного университета имени Франциска Скорины
Жогаль Светлана Ивановна – кандидат технических наук, доцент кафедры математических проблем управления и информатики Гомельского государственного университета имени Франциска Скорины
Орлов Владимир Васильевич – кандидат технических наук, доцент кафедры вычислительной математики и программирования Гомельского государственного университета имени Франциска Скорины
Скачать PDF (249 КБ)
Рябченко Н.В. Тригонометрические аппроксимации Паде специальных функций
Для функций Hγ=∑∞k=1 sin kx / (γ)k, где (γ)k =γ (γ +1) … (γ + k-1) и их тригонометрических аппроксимаций Паде πtn,m(x; Hγ) найдена асимптотика убывания разности Hγ (x)- πtn,m(x;Hγ) в случае, когда 0 ≤ m ≤ m(n), m(n) = о(n) и n→∞. При сделанных предположениях установлено, что тригонометрические аппроксимации Паде πtn,m(x; Hγ) приближают функцию Hγ равномерно на R со скоростью, асимптотически равной наилучшей.
Ключевые слова: аппроксимации Паде, асимптотические равенства, наилучшие равномерные приближения, тригонометрические аппроксимации.
Рябченко Наталья Валерьевна – аспирантка кафедры математического анализа и дифференциальных уравнений Гомельского государственного университета имени Франциска Скорины
Скачать PDF (244 КБ)
Селькин В.М., Близнец И.В., Закревская В.С. Критерий σ-разрешимости конечной группы
На протяжении всей статьи все группы конечны и G всегда обозначает конечную группу. Более того, σ является некоторым разбиением множества всех простых чисел P, т. е. σ={σi | i ∈ I} где P = ∪i ∈ I σi и σi∩σj = ∅ для всех i≠j. Множество подгрупп
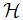 группы G называется полным холловым σ-множествомG, если каждый член ≠1 множества
группы G называется полным холловым σ-множествомG, если каждый член ≠1 множества
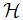 является холловой σi-подгруппой группы G для некоторого i и
является холловой σi-подгруппой группы G для некоторого i и
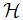 содержит ровно одну холлову σi-подгруппу группы G для каждого i. Подгруппа A группы G называется: σ-перестановочной в G, если G обладает полным холловым σ-множеством
содержит ровно одну холлову σi-подгруппу группы G для каждого i. Подгруппа A группы G называется: σ-перестановочной в G, если G обладает полным холловым σ-множеством
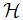 таким, что AHx = HxA для всех
таким, что AHx = HxA для всех
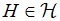 и всех x∈G; σ-субнормальной в G, если в G имеется цепь подгрупп A=A0≤A1≤...≤Ai=G такая, что либо
и всех x∈G; σ-субнормальной в G, если в G имеется цепь подгрупп A=A0≤A1≤...≤Ai=G такая, что либо
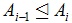 либо
либо
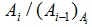 является σ-примарной группой для всех i=1,...,t. Подгруппа A группы G является слабо σ-перестновочной в G, если в G имеются σ-перестановочная подгруппа S и σ-субнормальная подгруппа T такие, что G=AT и A∩T≤S≤A. В данной работе доказывается, что если в каждой максимальной цепи M3<M2<M1<M0=G группы G длины 3 хотя бы одна из подгрупп M3, M2 или M1 является либо субмодулярной, либо слабо σ-перестановочной в G, то G σ-разрешима.
является σ-примарной группой для всех i=1,...,t. Подгруппа A группы G является слабо σ-перестновочной в G, если в G имеются σ-перестановочная подгруппа S и σ-субнормальная подгруппа T такие, что G=AT и A∩T≤S≤A. В данной работе доказывается, что если в каждой максимальной цепи M3<M2<M1<M0=G группы G длины 3 хотя бы одна из подгрупп M3, M2 или M1 является либо субмодулярной, либо слабо σ-перестановочной в G, то G σ-разрешима.
Ключевые слова: конечная группа, σ-разрешимая группа, σ-субнормальная подгруппа, σ-перестановочная подгруппа, слабо σ-перестановочная подгруппа, модулярная подгруппа.
Селькин Вадим Михайлович – доктор физ.-мат. наук, доцент, зав. кафедрой алгебры и геометрии Гомельского государственного университета имени Франциска Скорины
Близнец Игорь Васильевич – кандидат физ.-мат. наук, доцент кафедры фундаментальной и прикладной математики Гомельского государственного университета имени Франциска Скорины
Закревская Виктория Сергеевна – аспирантка факультета математики и технологий программирования Гомельского государственного университета имени Франциска Скорины
Скачать PDF (317 КБ)
ТЕХНИКА
Ильющенко А.Ф., Кривонос О.К., Чорный А.Д. Способ определения баллистического коэффициента оперенного аэродинамического объекта
Рассмотрены возможные способы и предложена методика вычислительного эксперимента для расчета аэродинамических характеристик оперенных аэродинамических объектов. Проведена ее верификация на объекте простой формы (конус + цилиндр) с последующим согласованием полученных значений для исследуемого объекта с доступными
экспериментальными данными. Методом вычислительного эксперимента рассчитаны коэффициенты формы и баллистические коэффициенты в зависимости от числа Маха для аэродинамического объекта с двумя формами головной части. Баллистические коэффициенты получены по законам 1943 года и 1958 года, а также по закону Сиаччи в виде функций от числа Маха. Полученные значения коэффициентов будут использованы в расчетах исходных данных для пуска аэродинамического объекта.
Ключевые слова: аэродинамический объект, коэффициент лобового сопротивления, моделирование обтекания тела, баллистический коэффициент.
Ильющенко Александр Федорович – доктор технических наук, профессор, член-корреспондент НАН Беларуси, генеральный директор Государственного научно-производственного объединения порошковой металлургии, Минск
Кривонос Олег Константинович – кандидат военных наук, доцент, заместитель генерального директора Государственного научно-производственного объединения порошковой металлургии, Минск
Чорный Андрей Дмитриевич – кандидат физико-математических наук, доцент, заведующий лабораторией турбулентности Института тепло- и массообмена имени А.В. Лыкова Национальной академии наук Беларуси, Минск
Скачать PDF (1,01 МБ)
ИНФОРМАТИКА
Садов С.В., Демиденко О.М., Ерофеев И.А., Садов В.С. Алгоритмы определения эмоций заинтересованности у обучаемых по мимике лица
Представлены разработанные алгоритмы определения эмоций заинтересованности у обучаемых по мимике с использованием ключевых точек на изображении лица, позволяющие организовать в реальном времени эффективный контроль за качеством учебного процесса при дистанционных формах обучения.
Ключевые слова: алгоритмы, эмоции, изображения лица, лицевые ориентиры, классификатор.
Садов Сергей Васильевич – аспирант кафедры интеллектауальных систем факультета радиофизики и компьютерных технологий Белорусского государственного университета, Минск
Демиденко Олег Михайлович – доктор технических наук, профессор, проректор по научной работе Гомельского государственного университета имени Франциска Скорины
Ерофеев Илья Александрович – студент факультета радиофизики и компьютерных технологий Белорусского государственного университета, Минск
Садов Василий Сергеевич – кандидат технических наук, доцент, профессор кафедры интеллектауальных систем факультета радиофизики и компьютерных технологий Белорусского государственного университета, Минск
Скачать PDF (1,61 МБ)
|












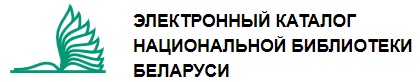
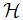 группы G называется полным холловым σ-множествомG, если каждый член ≠1 множества
группы G называется полным холловым σ-множествомG, если каждый член ≠1 множества
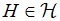 и всех x∈G; σ-субнормальной в G, если в G имеется цепь подгрупп A=A0≤A1≤...≤Ai=G такая, что либо
и всех x∈G; σ-субнормальной в G, если в G имеется цепь подгрупп A=A0≤A1≤...≤Ai=G такая, что либо
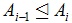 либо
либо
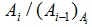 является σ-примарной группой для всех i=1,...,t. Подгруппа A группы G является слабо σ-перестновочной в G, если в G имеются σ-перестановочная подгруппа S и σ-субнормальная подгруппа T такие, что G=AT и A∩T≤S≤A. В данной работе доказывается, что если в каждой максимальной цепи M3<M2<M1<M0=G группы G длины 3 хотя бы одна из подгрупп M3, M2 или M1 является либо субмодулярной, либо слабо σ-перестановочной в G, то G σ-разрешима.
является σ-примарной группой для всех i=1,...,t. Подгруппа A группы G является слабо σ-перестновочной в G, если в G имеются σ-перестановочная подгруппа S и σ-субнормальная подгруппа T такие, что G=AT и A∩T≤S≤A. В данной работе доказывается, что если в каждой максимальной цепи M3<M2<M1<M0=G группы G длины 3 хотя бы одна из подгрупп M3, M2 или M1 является либо субмодулярной, либо слабо σ-перестановочной в G, то G σ-разрешима.