|
|
PROBLEMS OF PHYSICS, MATHEMATICS AND TECHNICS N3 (28) 2016
PHYSICS
Vasilets V.K., Khmyl A.A., Kuzmar I.I., Dezhkunov N.V. The influence of electric current parameters and ultrasonic oscillations on the microstructure and properties of Sn-Bi electroplating coatings
The coeffect of electrolysis mode and ultrasonic oscillations on microstructure, composition and properties of Sn-Bi coatings is considered. It was found that the use of non-stationary electrolysis and ultrasonic stimulation to optimize the deposition parameters, with which it is possible to avoid the deterioration of solderability while improving sludge quality.
Keywords: lead-free alloys, tin-bismuth alloy, non-stationary electrolysis, ultrasonic oscillations, microstructure, solderability, electrical resistivity.
V.K. Vasilets – Belarusian State University of Informatics and Radioelectronics, Minsk
A.A. Khmyl – Belarusian State University of Informatics and Radioelectronics, Minsk
I.I. Kuzmar – Belarusian State University of Informatics and Radioelectronics, Minsk
N.V. Dezhkunov – Belarusian State University of Informatics and Radioelectronics, Minsk
Download PDF (1,47 MB)
Ovsiyuk Å.Ì., Red'ko À.N., Kisel V.V., Red'kov V.Ì. Isotopic doublet of the Dirac particles in presence of the non-Abelian monopole: the Pauli approximation
For the doublet of Dirac particles in presence of external non-Abelian fields, a non-relativistic Pauli equation is constructed. It is detailed for the case of the Bogomolny – Prasad – Sommerfeld monopole potentials. The problem of existence of bound states in the system is studied. Comparison of the behavior of the Dirac particles doublet in three spaces of constant curvature: Euclid, Lobachevsky, and Rie-mann, is performed, from where it follows that the known nonsingular monopole solution usually used for the case of Minkowski space is the application of a mathematical possibility more naturally related to the Lobachevsky space model. Within that treatment, in all three space models, no bound states for the doublet of fermions in the non-Abelian monopole potential exist.
Keywords: doublet of fermions, non-Abelian monopole, Pauli approximation, spaces of constant curvature, bound states.
Å.Ì. Ovsiyuk – I.P. Shamyakin Mosyr State Pedagogical University
À.N. Red'ko – M. Tank Belarusian State Pedagogical University, Minsk
V.V. Kisel – Belarusian State University of Informatics and Radioelectronics, Minsk
V.Ì. Red'kov – B.I. Stepanov Institute of Physics National Academy of Sciences of Belarus, Minsk
Download PDF (313 KB)
Khoroshko V.V. Production route of solar cells based on thin films of chalcogenides
Route production of thin-film solar cells is presented and justified. This route allows fulfilling the requirements for the quality of the resulting materials of the design Mo/absorber layer/CdS/ZnO/Al-Ni.
Keywords: CuxInxZn2-2xSe2, thin films, solar cells, physical characteristics, efficiency.
V.V. Khoroshko – Belarusian State University of Informatics and Radioelectronics, Minsk
Download PDF (285 KB)
Shushkevich G.Ch. Scattering of the field of the electrical dipole on thin unclosed spherical shell ànd bi-isotropic ball. Analytical approach
The analytical solution of axially symmetric boundary problem of process scattering of electromagnetic field of electric dipole on bi-isotropic ball is constructed. The dipole is located inside thin unclosed spherical shell. The formula for calculating directive pattern of electric field is received. The graphics of directive pattern for some parameters of the problem are constructed.
Keywords: electric dipole, Maxwell's equations, vector spherical wave functions, dual series equations, directive pattern of the electric field.
G.Ch. Shushkevich – Y. Kupala Grodno State University
Download PDF (431 KB)
MATHEMATICS
Borodich T.V. On solvability of a group with Hall supplements to normalizers of isolated subgroups
Let G be finite group and 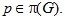 Suppose that for all 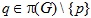 normalizer Sylow q-subgroups has nilpotent Hall supplement. Under these assumptions, prove that G is solvable.
Keywords: finite group, soluble group, nilpotent group, Hall subgroup, Sylow subgroup, normalizer.
T.V. Borodich – Department of Mathematics, F. Skorina Gomel State University
Download PDF (252 KB)
Monakhov V.S., Chirik I.K. Finite factorised groups whose factors are subnormal supersolvable subgroups
New criteria of supersolvability for a finite group which is factorised as a product of supersoluble subgroups are obtained. Some applications to the factorization by F( G)-subnormal subgroups are presented.
Keywords: finite group, supersolvable group, derived subgroup, subnormal subgroup, factorised group.
V.S. Monakhov – Department of Mathematics, F. Skorina Gomel State University
I.K. Chirik – University of Civil Protection of the Ministry for Emergency Situations of the Republic of Belarus
Download PDF (297 KB)
Musafirov E.V. Admissible perturbations of Langford system
The set of three-dimensional systems of nonautonomous ordinary differential equations for which the reflecting function coincides with reflecting function of the Langford system is obtained. It allows comparing the qualitative behavior of solutions of the obtained systems and Langford system.
Keywords: reflecting function, system of ordinary differential equations, Hopf bifurcation, periodic solution.
E.V. Musafirov – Y. Kupala Grodno State University
Download PDF (428 KB)
Pranevich A.F. Poisson theorem of building autonomous integrals for autonomous systems of total differential equations
The autonomous system of total differential equations and corresponding to it Hamiltonian differential system are considered. The analytical relations (the existence of first integrals and partial solutions, fulfillment of conditions of completely solvability) between these differential systems are established. Using these relations, the Poisson theorem of building autonomous first integrals for autonomous system of total differential equations is proved and statements of the existence of additional autonomous first integrals for this system are obtained.
Keywords: system of total differential equations, first integral, Poisson theorem.
A.F. Pranevich – Y. Kupala Grodno State University
Download PDF (269 KB)
Semenchuk V.N. Finite groups with generalized subnormal Sylow subgroups
The structure of finite groups every Sylow subgroup of which is generalized subnormal is studied.
Keywords: saturated formation, hereditary formation, soluble group, subnormal subgroup, generalized subnormal subgroup.
V.N. Semenchuk – Department of Mathematics, F. Skorina Gomel State University
Download PDF (231 KB)
Sinitsa D.A., Rizhik V.N. On one generalization of finite -nilpotent groups
Let G be a finite group. Let 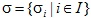 be a partition of the set of all primes  and n an integer. Let 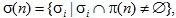 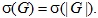
A set 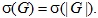 of subgroups of G is said to be a complete Hall
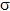 -set of G if every member of 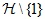 is a Hall 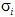 -subgroup of G for some 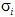 and 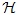 contains exact one Hall 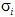 -subgroup of G for every 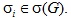 If G possesses a complete Hall 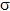 -set, then it is said to be 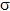 -full. A subgroup A of G is called: (i) a 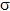 -Hall subgroup of G if 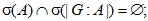 (ii) 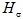 -normally embedded in G if A is a 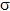 -Hall subgroup of some normal subgroup of G. In this paper, we study 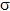 -full groups G whose all subgroups are 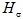 -normally embedded in G.
Keywords: finite group, 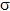 -Hall subgroup, -Hall subgroup, 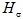 -normally embedded subgroup, -normally embedded subgroup, 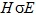 -group. -group.
D.A. Sinitsa – Department of Mathematics, F. Skorina Gomel State University
V.N. Rizhik – Bryansk State Agrarian University, Kokino
Download PDF (280 KB)
Shpak D.S., Trifonova I.V. The method of application of nonlinear evolution operators for solution of dynamical systems
The solution of many technical, physical and mathematical problems is closely related to the study of nonlinear equations and systems. A description of these processes contributed to the establishment and development of systems theory, the development of the mathematical apparatus of the “input-output” using the nonlinear evolution operators. The nonlinear evolution operators of the first and the second multiplicities are dealt in this paper. The method of their application for solution of dynamical systems with generalized characteristics is described. This method is based on the algorithm of constructing asymptotically inverse nonlinear evolution operators.
Keywords: evolution operator, impulse response, spectral response, multipole, system, asymptotically reverse evolution operator.
D.S. Shpak – Y. Kupala Grodno State University
I.V. Trifonova – Y. Kupala Grodno State University
Download PDF (242 KB)
Shukur Ali A., Arhipenko O.A. Resolvent of boundary value problem for the difference equation
Boundary value problem for the difference equation 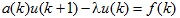 with spectral parameter 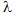 is considered. The condition of the existence of the right sided resolvents of the above problem in the space 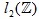 is given. The resolvent is constructed.
Keywords: right-side resolvent, discrete weighted shift operator, Risze projection.
Ali A. Shukur – Belarusian State University, Minsk
O.A. Arhipenko – Belarusian State University, Minsk
Download PDF (265 KB)
INFORMATION SCIENCE
Demidenko O.M., Divakov N.N., Chechet P.L. Tuning of DNS for simultaneous use on the IPv4 and IPv6 nodes
The problem of simultaneous use of DNS on the IPv4 and IPv6 nodes is considered; the network diagram that simulates the operation of DNS-servers is offered; some situations are analyzed.
Keywords: IPv6, switch, PC, DNS, Cisco packet Tracer, IP address.
O.M. Demidenko – F. Skorina Gomel State University
N.N. Divakov – F. Skorina Gomel State University
P.L. Chechet – F. Skorina Gomel State University
Download PDF (413 KB)
Miniailau U.S. Detection of elliptical sentences using classification algorithms
The problem of correct processing of elliptic structures in the automatic syntactic parsing of natural language is studied. Capabilities for detection of elliptical sentences are considered in details.
Keywords: automatic syntactic analysis, ellipsis, classification.
U.S. Miniailau – Lomonosov Moscow State University
Download PDF (235 KB)
Osipenko A.N., Osipenko N.B., Slepianok Y.À. Automation of diagnostic potential of human qualities when choosing a profession
The version of the pilot project of the automated Express-diagnostics of suitable human spheres of activity and professions is described. The draft is based on the concept of the information environment that can accumulate all sorts of characteristics and results of diagnostic testing in a universal fractal matrix of the person. The algorithm of projection of the test results in a generic matrix on the example of the description of the potential qualities of a person by using a square of Pythagoras. Verification of the computer program has demonstrated its performance and viability.
Keywords: sphere of activities, profession, algorithm of Pythagoras.
A.N. Osipenko – P.O. Sukhoi Gomel State Technical University
N.B. Osipenko – Department of Mathematics, F. Skorina Gomel State University
Y.À. Slepianok – Department of Mathematics, F. Skorina Gomel State University
Download PDF (286 KB)
|












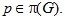 Suppose that for all
Suppose that for all 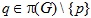 normalizer Sylow q-subgroups has nilpotent Hall supplement. Under these assumptions, prove that G is solvable.
normalizer Sylow q-subgroups has nilpotent Hall supplement. Under these assumptions, prove that G is solvable.
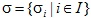 be a partition of the set of all primes
be a partition of the set of all primes 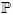 and n an integer. Let
and n an integer. Let 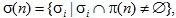
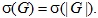 A set
A set 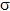 -set of G if every member of
-set of G if every member of 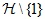 is a Hall
is a Hall 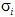 -subgroup of G for some
-subgroup of G for some 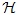 contains exact one Hall
contains exact one Hall 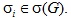 If G possesses a complete Hall
If G possesses a complete Hall 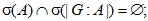 (ii)
(ii) 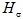 -normally embedded in G if A is a
-normally embedded in G if A is a 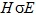 -group.
-group.
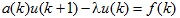 with spectral parameter
with spectral parameter 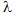 is considered. The condition of the existence of the right sided resolvents of the above problem in the space
is considered. The condition of the existence of the right sided resolvents of the above problem in the space 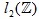 is given. The resolvent is constructed.
is given. The resolvent is constructed.