|
|
PROBLEMS OF PHYSICS, MATHEMATICS AND TECHNICS N2 (3) 2010
PHYSICS
Maksimenko N.V., Kuchin S.M. Spectral problem of the Klein-Gordon-Fock equation
The eigenvalues and eigenfunctions of the relativistic bound system based on Klein-Gordon-Fock equation with a mixed, scalar-vector coupling are determined.
Keywords: relativistic bound system, eigenvalues and eigenfunctions.
N.V. Maksimenko – Department of Physics, F. Skorina Gomel State University, Gomel, Belarus
S.M. Kuchin – Department of Physics and Mathematics I.G. Petrovski Briansk State University, Briansk, Russia
Download PDF (318 KB)
Yarmolenko M.A., Rogachåv A.A., Rogachåv A.V., Gorbachyov D.L. Molecular structure and morphology of the polyethylene coatings alloyed when forming from gas phase by low-molecular compound
The molecular structure and morphology of the polyethylene coatings, which inherently contain functional additions, are defined. It was established that the coatings that were received by electron beam dispersion have higher trans-vinylene nonsaturation and bigger size of permolecular formations in comparison with the coatings that were received by thermal dispersion. On the basis of the data analysis of the influence of the filling material nature on molecular structure of the compositional layers, formed by electron beam method, an assumption of the influence of ion-molecular processes alongside with free radical processes on secondary polymerization was made.
Keywords: morphology, molecular structure, polyethylene, infrared spectroscopy, compositional coatings.
M.A. Yarmolenko – Department of Physics, F. Skorina Gomel State University, Gomel, Belarus
A.A. Rogachev – Department of Physics, F. Skorina Gomel State University, Gomel, Belarus
A.V. Rogachev – Rector of F. Skorina Gomel State University, Gomel, Belarus
D.L. Gorbachyov – Department of Physics, F. Skorina Gomel State University, Gomel, Belarus
Download PDF (1,18 MB)
MATHEMATICS
Vasilyev A.F., Vasilyeva T.I., Tyutyanov V.N. On finite groups similar to supersoluble groups
A subgroup H of G is called P-subnormal in G if either H = G or there is a chain 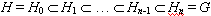 such that
|Hi+1 : Hi|
is a prime number for every i = 0, 1, … , n-1. For the set of such that
|Hi+1 : Hi|
is a prime number for every i = 0, 1, … , n-1. For the set of  primes the properties of primes the properties of 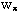 -supersoluble groups G, i.e. groups for which for every -supersoluble groups G, i.e. groups for which for every 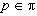 Sylow p-subgroup is P-subnormal in G are investigated. It is proved that the class of all Sylow p-subgroup is P-subnormal in G are investigated. It is proved that the class of all 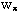 -supersoluble groups is a normally hereditary formation, and the class of all soluble -supersoluble groups is a normally hereditary formation, and the class of all soluble 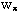 -supersoluble groups is a hereditary saturated formation. The properties of the groups, which are the product of P-subnormal subgroups are obtained. -supersoluble groups is a hereditary saturated formation. The properties of the groups, which are the product of P-subnormal subgroups are obtained.
Keywords: finite group, P-subnormal subgroup, 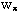 -supersoluble group, formation, -supersoluble group, formation,  -saturated formation. -saturated formation.
A.F. Vasilyev – Department of Mathematics, F. Skorina Gomel State University, Gomel, Belarus
T.I. Vasilyeva – Belarusion State University of Transport, Gomel, Belarus
V.N. Tyutyanov – Department of Mathematics, F. Skorina Gomel State University, Gomel, Belarus
Download PDF (436 KB)
Vasilyev V.A., Skiba A.N. New characterizations of finite soluble groups
A subgroup H of a group G is called modular in G if H is a modular element (in sense of Kurosh) of the lattice L(G) of all subgroups of G. The subgroup of H generated by all modular subgroups of G contained in
H is called the modular core of H and denoted by 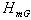 . In the paper, we introduce the following concepts. A subgroup H of a group G is called m-supplemented (m-subnormal) in G if there exists a subgroup (a subnormal subgroup respectively) K of G such that G=HK and . In the paper, we introduce the following concepts. A subgroup H of a group G is called m-supplemented (m-subnormal) in G if there exists a subgroup (a subnormal subgroup respectively) K of G such that G=HK and 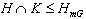 . We proved the following theorems. . We proved the following theorems.
Theorem A. A group G is soluble if and only if each Sylow subgroup of G is m-supplemented in G.
Theorem B. A group G is soluble if and only if every its maximal subgroup is m-subnormal in G.
Keywords: finite group, soluble group, subnormal subgroup, modular subgroup, modular core, m-supplemented subgroup, m-subnormal subgroup.
V.A. Vasilyev – Department of Mathematics, F. Skorina Gomel State University, Gomel, Belarus
A.N. Skiba – Department of Mathematics, F. Skorina Gomel State University, Gomel, Belarus
Download PDF (416 KB)
Gabasov R., Kuzmenkov D.S. Optimal control problem of a thermal process in the rod under uncertainties
An optimal control problem of a thermal process in the rod under uncertainties is considered. The proposed solution method is the reduction to linear system optimal observation problems and optimal control of the determinate system on the obtained evaluations. Operating algorithm of the optimal allocation regulator that forms optimal feedback in real time current values is described.
Keywords: thermal process, optimal feedback on allocation, optimal control problem, principle of divisibility.
R. Gabasov – Department of Applied Mathematics and Information Science, Belarusian State University, Minsk, Belarus
D.S. Kuzmenkov – Department of Mathematics, F. Skorina Gomel State University, Gomel, Belarus
Download PDF (405 KB)
Lubochkin A.V. Solution of the classical regulation problem by optimal controls of linear-quadratic problems
The basic problem of the classical regulation theory in the bounded control class is considered. Optimal control methods are used to construct the regulator work algorithm. These methods perform feedback implementation in the real-time mode. The feedback transfers the system from one equilibrium condition vicinity into another one with high transient quality. It stabilizes the system according to the new equilibrium condition. To solve the problem the feedback optimal control realization of linear-quadratic problem with restrictions is suggested. The results are illustrated with the example of the linear dynamical system regulation of the fourth order.
Keywords: dynamic system, regulation problem, bounded stabilizing feedback, auxiliary optimal control problem, regulator.
A.V. Lubochkin – Department of Mathematics, F. Skorina Gomel State University, Gomel, Belarus
Download PDF (439 KB)
Mozharovsky V.V., Marjina N.A. Mathematical modeling of nano-contact interaction of orthotropic bodies
The elastic problem of application of the theory of contact interaction in system «scanning probe – orthotropic sample» for both homogeneous elastic body and orthotropic coating is considered. Analytical dependences and the graphs facilitating search and finding contact.
Keywords: contact, orthotropic body, nano-contact, coating, composite, model.
V.V. Mozharovsky – Department of Mathematics, F. Skorina Gomel State University, Gomel, Belarus
S.A. Marjina – Belarusion State University of Transport, Gomel, Belarus
Download PDF (433 KB)
Fan Cheng, Jianhong Huang, Wenjuan Niu, Lifang Ma The influence of s-c-permutably embedded subgroups on the structure of finite groups
A subgroup H of a group G is said to be s-c-permutably embedded in G if every Sylow subgroup of H is a Sylow subgroup of some s-conditionally permutable subgroup of G. In this paper, some new characterizations for a finite group to be p-supersoluble or p-nilpotent are obtained under the assumption that some of its maximal subgroups or 2-maximal subgroups of Sylow subgroups are s-c-permutably embedded. A series of known results are generalized.
Keywords: finite group, s-c-permutably embedded subgroups, 2-maximal subgroups, Sylow subgroup, p-supersoluble group, p-nilpotent group.
Fan Cheng – Department of Mathematics, Xuzhou Normal University, Xuzhou, China
Jianhong Huang – Department of Mathematics, Xuzhou Normal University, Xuzhou; Department of Mathematics, University of Science and Technology of China, China
Wenjuan Niu – Department of Mathematics, Xuzhou Normal University, Xuzhou, China
Lifang Ma – Department of Mathematics, Xuzhou Normal University, Xuzhou, China
Download PDF (475 KB)
TECHNICS
Golosov D.A., Melnikov S.N., Kundas S.P., Dostanko A.P. Prediction of targets erosion in magnetron sputtering systems
The method of prediction of targets erosion in magnetron sputtering systems is suggested. The method based on the evaluation of the effective ionization zone for the working gas atoms, approximate concentration of the charged particles, and an assumption that the concentration of ionizing events at each point of the plasma volume is proportional to the horizontal component of magnetic field intensity to the magnetic field intensity square. For the practical implementation of the suggested model the software tool TargProf has been developed capable of calculating the magnetic field configuration with the aid of the ELCUT package, generating output data matrices, and analyzing the results obtained. The TargProf enables to predict the profile of the erosion zone on a target at the stage of the magnetron system design with the error not exceeding 15–20% (depending on the magnetron configuration).
Keywords: magnetron sputtering system, erosion zone, plasma discharge, magnetic field, modeling of discharge.
D.A. Golosov – Belarusian State University of Informatics and Radioelectronics, Minsk, Belarus
S.N. Melnikov – Belarusian State University of Informatics and Radioelectronics, Minsk, Belarus
S.P. Kundas – Rector of International Sakharov Environmental University, Minsk, Belarus
A.P. Dostanko – Department of Computer-Aided Design Belarusian State University of Informatics and Radioelectronics, Minsk, Belarus
Download PDF (653 KB)
Muravsky A.A., Agabekov V.E., Malashko P.M., Matsur A.I. New optical functional materials based on alkaline metalls salts of 5-(2-{4-[2-(3-carboxy-4-hydroxyphenyl)diazenyl]phenyl}diazenyl)-2-hydroxybenzenecarboxylic acid
New functional materials – layers of nanosized thickness based on alkaline salts of azodyes are developed. The layers form hydrophilic photoinduced anisotropic surfaces for epitaxial growth and photoalignment of liquid crystals – the mesogenic systems. It is shown that sodium and potassium salts of 5-(2-{4-[2-(3-carboxy-4-hydroxyphenyl)diazenyl]phenyl}diazenyl)-2-hydroxybenzenecarboxylic acid demonstrate marked difference in reorientation dynamics of LC photoalignment direction. Based on the new materials the optically addressable liquid crystal indicator is realized, and the possibility of creation of polarization optical logic gate is demonstrated.
Keywords: photoalignment, organic epitaxy, nanolayer, functional materials.
A.A. Muravsky – Institute of Chemistry of New Materials NAS Belarus, Minsk, Belarus
V.E. Agabekov – Director of Institute of Chemistry of New Materials of the National Academy of Sciences of Belarus, Minsk, Belarus
P.M. Malashko – Institute of Chemistry of New Materials NAS Belarus, Minsk, Belarus
A.I. Matsur – Institute of Chemistry of New Materials NAS Belarus, Minsk, Belarus
Download PDF (2,7 MB)
Sukach E.I., Ratobylskaya D.V., Mereja V.L. Probability-algebraic simulation of the characteristics of mechanical systems reliability
In the paper the probability-algebraic simulation method allowing investigation the reliability of mechanical systems is considered. The method takes into account the probability nature of the damages accumulated by the system components. It demonstrates the statistical property of damages of the interference while in service systems.
Keywords: probability-algebraic simulation, reliability of mechanical system, algebra, uncertainty of the data, uncertainty of operations.
E.I. Sukach – Department of Mathematics, F. Skorina Gomel State University, Gomel, Belarus
D.V. Ratobylskaya – Department of Mathematics, F. Skorina Gomel State University, Gomel, Belarus
V.L. Mereja – Department of Mathematics, F. Skorina Gomel State University, Gomel, Belarus
Download PDF (344 KB)
Zhu Peng, Fedosenko N.N., Piliptsov D.G., Bekarevich R.V. Study of the preparation CuO and boron films
The use of ion beam source sputtering, CuO and B films were deposited successively. The deposition speeds are 11 nm/min and 11.8 nm/min, respectively. The purity and morphology of the as-prepared films were investigated by power X-ray diffraction and atomic force microscopy. Thus it is can be seen that the sizes of the films were more homogeneous in B than CuO.
Keywords: atomic force microscopy, boron, ion beam source sputtering, hot isostatic pressing, X-ray diffraction
Zhu Peng – Nanjing University of Science and Technology, Nanjing, China
N.N. Fedosenko – Department of Physics, F. Skorina Gomel State University, Gomel, Belarus
D.G. Piliptsov – Department of Physics, F. Skorina Gomel State University, Gomel, Belarus
R.V. Bekarevich – Department of Physics, F. Skorina Gomel State University, Gomel, Belarus
Downloads PDF (605 KB)
|












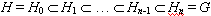 such that
such that
 primes the properties of
primes the properties of 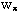 -supersoluble groups
-supersoluble groups 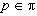 Sylow
Sylow 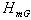 . In the paper, we introduce the following concepts. A subgroup
. In the paper, we introduce the following concepts. A subgroup 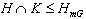 . We proved the following theorems.
. We proved the following theorems.