|
|
ПРОБЛЕМЫ ФИЗИКИ, МАТЕМАТИКИ И ТЕХНИКИ №3 (40) 2019
ФИЗИКА
Джоу Б., Пилипцов Д.Г., Цзян С., Кулеш Е.А., Руденков А.С. Бор-углеродные покрытия:
методы получения, особенности структуры и механических свойств
Рассмотрены основные методы формирования покрытий на основе бора и углерода. Описаны основные фазовые состояния, образующиеся в процессе синтеза таких покрытий. Уделено внимание анализу взаимосвязи структуры и механических свойств. Предложена методика и устройство для осаждения бор-углеродных покрытий из совмещенных потоков углеродной плазмы, формируемой за счет электроискрового испарения графитового катода импульсной дугой, и ионов бора, генерируемых в результате испарения мишени импульсным лазерным излучением.
Ключевые слова: углеродные покрытия, легирование, бор, микротвердость, износостойкость, коэффициент трения.
Б. Джоу – Нанкинский университет науки и технологии
Пилипцов Дмитрий Геннадьевич – кандидат технических наук, доцент, ведущий научный сотрудник НИС Гомельского государственного университета им. Ф. Скорины
С. Цзян – Нанкинский университет науки и технологии
Кулеш Екатерина Александровна – младший научный сотрудник НИС Гомельского государственного университета им. Ф. Скорины
Руденков Александр Сергеевич – кандидат технических наук, старший научный сотрудник НИС Гомельского государственного университета им. Ф. Скорины
Скачать PDF (427 КБ)
Кулак Г.В., Крох Г.В., Николаенко Т.В. Акустооптическая диагностика ультразвуковых волн лэмба бесселевыми световыми пучками в кристаллах силленитов
Показано, что для бесселевого светового пучка возможно раздельное наблюдение изотропной и анизотропной брэгговской дифракции циркулярно поляризованных волн на модах Лэмба в гиротропных кубических кристаллах. При этом эффективное акустооптическое взаимодействие в прошедших и отраженных дифракционных порядках реализуется в узком интервале толщин слоя вблизи толщины отсечки моды. Наибольший интерес для акустооптической диагностики мод Лэмба представляет нулевая мода бесселевого светового пучка при условии изотропной дифракции циркулярно поляризованных волн при точном поперечном фазовом синхронизме дифрагированных пучков.
Ключевые слова: плоскопараллельный слой, волны Лэмба, акустооптическая дифракция, гиротропный кубический кристалл, коэффициенты отражения и пропускания.
Кулак Геннадий Владимирович – профессор Мозырского государственного педагогический университета им. И.П. Шамякина
Крох Григорий Васильевич – Мозырский государственный педагогический университет им. И.П. Шамякина
Николаенко Татьяна Викторовна – доцент Мозырского государственного педагогический университета им. И.П. Шамякина
Скачать PDF (459 КБ)
Овсиюк Е.М., Коральков А.Д. Релятивистская частица со спином 1 в кулоновском поле, квантовые состояния с минимальным угловым моментом j=0 в моделях Лобачевского и Римана
Ранее были исследованы нерелятивистские уравнения для векторной частицы во внешнем кулоновском поле в пространствах Лобачевского и Римана, при этом использовалось модифицированное уравнение Даффина – Кеммера, что позволило в нерелятивистском приближении получить три несвязанных уравнения для отдельных радиальных функций и найти три серии уровней энергии. Однако состояния с минимальным значением j=0 полного углового момента при этом не рассматривались. В настоящей работе исследованы состояния с j=0, при этом для упрощения математической задачи нет необходимости переходить к нерелятивистскому приближению. В обеих пространственных моделях применяются обычное и модифицированное уравнения Даффина – Кеммера, построены решения уравнений в гипергеометрических функциях и в трансцендентных общих функциях Гойна. В каждой из пространственных моделей эти решения соответствуют незначительно различающимся спектрам. Можно предположить, что аналогичное свойство имеет место и для больших значений полного момента j, даже если известны решения только модифицированного нерелятивистского уравнения Даффина – Кемера.
Ключевые слова: частица со спином 1, уравнение Даффина – Кеммера, кулоновский потенциал, минимальные значения полного углового момента, уравнение Гойна, точное решение, энергетический спектр.
Овсиюк Елена Михайловна – кандидат физ.-мат. наук, доцент кафедры физики и математики Мозырского государственного педагогического университета им. И.П. Шамякина
Коральков Артем Дмитриевич – студент физико-инженерного факультета Мозырского государственного педагогического университета им. И.П. Шамякина
Скачать PDF (285 КБ)
Семченко И.В., Хахомов С.А., Самофалов А.Л., Фаняев И.А., Михалко И.С., Сонг Я., Фан Ш., Ванг Дж. Разработка двухстороннего неотражающего поглотителя микроволн на основе метаматериалов с прямоугольными омега-элементами
Целью статьи является выявление закономерностей взаимодействия микроволн с метаматериалами, состоящими из прямоугольных омега-элементов, а также разработка одностороннего и двустороннего «идеального» поглотителя микроволн на основе таких структур.
Ключевые слова: омега-элемент, метаматериал, поглотитель, микроволновый диапазон, отражение, поглощение.
Семченко Игорь Валентинович – доктор физ.-мат. наук, профессор, проректор по учебной работе Гомельского государственного университета им. Ф. Скорины
Хахомов Сергей Анатольевич – доктор физ.-мат. наук, ректор Гомельского государственного университета им. Ф. Скорины
Самофалов Андрей Леонидович – кандидат физ.-мат. наук, доцент, зам. декана факультета физики и информационных технологий Гомельского государственного университета им. Ф. Скорины
Фаняев Иван Александрович – кандидат физ.-мат. наук, старший преподаватель кафедры радиофизики и электроники факультета физики и информационных технологий Гомельского государственного университета им. Ф. Скорины
Михалко И.С. – Гомельский государственный университет им. Ф. Скорины
Я. Сонг – Нанкинский университет науки и технологий
Ш. Фан – Нанкинский университет науки и технологий
Дж. Ванг – Университет Цзяннань, Уси
Скачать PDF (2,42 МБ)
Сердюкова М.А., Сердюков А.Н. Массивное гравитационное поле в плоском пространстве-времени. II. Законы сохранения и гравитационная изменчивость инертной массы
Построен канонический тензор энергии-импульса и сформулированы законы сохранения энергии и импульса линейного массивного беспинового поля, адаптированного в качестве калибровочно-инвариантной модели гравитации в рамках специальной теории относительности. Показано, что общее требование положительной определенности плотности энергии любой физической реальности в случае гравитационного поля предопределяет его скалярную природу и далеко идущую гравитационную изменчивость инертной массы частиц материи.
Ключевые слова: массивная скалярная гравитация, энергия гравитационного поля, гравитационная изменчивость массы.
Сердюкова Мария Анатольевна – аспирант факультета физики и технологий программирования Гомельского государственного университета им. Ф. Скорины
Сердюков Анатолий Николаевич – член-корреспондент НАН Беларуси, доктор физико-математических наук, профессор кафедры оптики Гомельского государственного университета им. Ф. Скорины
Скачать PDF (319 КБ)
Сердюкова М.А. Массивное гравитационное поле в плоском пространстве-времени. III. Гравитационная зависимость радиоактивного распада
Показано, что изменение инертной массы нестабильных частиц (и атомных ядер) в скалярном гравитационном поле, возникающее в результате передачи полю части энергии покоя частиц, или, наоборот, при увеличении их энергии покоя за счет аккреции полевой энергии, сопровождается изменением темпов радиоактивного распада. Приложение скалярной теории гравитации к однородной вселенной предсказывает вековое ускорение темпов распада нестабильных ядер и частиц в современную эпоху. В космологическом масштабе времени этот процесс подтверждается наблюдаемым (1+z)-растяжением кривых блеска послесвечения сверхновых типа Ia, которое вызвано жестким гамма-излучением от распадающихся нестабильных нуклидов 56Ni and 56Co, созданных при взрыве аккрецирующих белых карликов.
Ключевые слова: массивная скалярная гравитация, переменная масса, радиоактивный распад.
Сердюкова Мария Анатольевна – аспирант факультета физики и технологий программирования Гомельского государственного университета им. Ф. Скорины
Скачать PDF (227 КБ)
Тимощенко Е.В., Юревич Ю.В. Расчёт эффективности бистабильного тонкоплёночного отражателя
Проведена расчётная оценка гистерезисных свойств отражения тонкого слоя на основе плотной резонансной среды на шкале мощности и линейной частотной отстройки внешнего сигнала. Определена роль подобного компактного резонансного отражателя в качестве модулятора добротности резонатора в лазерной схеме.
Ключевые слова: резонансное отражение, плотная резонансная среда, тонкие оптические плёнки, диполь-дипольное взаимодействие, квазирезонансная поляризация.
Тимощенко Елена Валерьевна – кандидат физ.-мат. наук, доцент Могилёвского государственного университета им. А.А. Кулешова
Юревич Юрий Владимирович – кандидат физ.-мат. наук, доцент Могилёвского государственного университета продовольствия
Скачать PDF (466 КБ)
Чжао Ц., Сонг Я., Ван Л., Семченко И.В., Самофалов А.Л. Проектирование многослойной структуры бифилярной спиральной антенны
Основываясь на опыте проектирования традиционной спиральной антенны и многослойной печатной платы, в данной статье предлагается многослойная бифилярная спиральная антенна на печатной плате, работающая в диапазоне C. Антенна состоит из нескольких симметричных металлических дуг, которые распределены по разным слоям и соединяются сквозными отверстиями. Результаты показывают, что антенна имеет низкопрофильное излучение с круговой поляризацией и лучшее согласование импедансов, обеспечивая новое решение для проектирования структуры многослойной антенны.
Ключевые слова: низкий профиль, бифилярная спиральная антенна, многослойная печатная плата, круговая поляризация.
Ц. Чжао – Нанкинский университет науки и технологий
Я. Сонг – Нанкинский университет науки и технологий
Л. Ван – Нанкинский университет науки и технологий
Семченко Игорь Валентинович – доктор физ.-мат. наук, профессор, проректор по учебной работе Гомельского государственного университета им. Ф. Скорины
Самофалов Андрей Леонидович – кандидат физ.-мат. наук, доцент, зам. декана факультета физики и информационных технологий Гомельского государственного университета им. Ф. Скорины
Скачать PDF (458 КБ)
МАТЕМАТИКА
Антоневич А.Б., Шагова Т.Г. Рациональные мнемофункции на окружности
Рассматривается способ вложения пространства распределений на окружности в алгебру мнемофункций, порожденный аналитическим представлением распределений. Выделена подалгебра мнемофункций на окружности, порожденная рациональными мнемофункциями. Приведено полное описание этой подалгебры: выделены образующие, сформулировано в явном виде правило умножения распределений в ней.
Ключевые слова: мнемофункция, аналитическое представление распределения, алгебра рациональных мнемофункций.
Антоневич Анатолий Борисович – доктор физ.-мат. наук, профессор кафедры функционального анализа и аналитической экономики механико-математического факультета Белорусского государственного университета
Шагова Татьяна Григорьевна – аспирант Белорусского государственного университета
Скачать PDF (325 КБ)
Дергачева И.М., Задорожнюк Е.А., Шабалина И.П. О p-сверхразрешимости одного класса конечных групп
Доказано следующее: конечная группа G p-сверхразрешима тогда и только тогда, когда она имеет нормальную подгруппу N с p-сверхразрешимой фактор-группой G/N такой, что либо N – p'-группа, либо p делит |N|, и |G:NG(L)| является степенью числа p для любой циклической p-подгруппы L из N порядка p или порядка 4 (если p=2 и в N силовская 2-подгруппа является неабелевой).
Ключевые слова: конечная группа, p-нильпотентная группа, p-сверхразрешимая группа.
Дергачева Ирина Михайловна – кандидат физ.-мат. наук, доцент Белорусского государственного университета транспорта
Задорожнюк Елена Андреевна – кандидат физ.-мат. наук, доцент Белорусского государственного университета транспорта
Шабалина Ирина Петровна – кандидат физ.-мат. наук, доцент Белорусского государственного университета транспорта
Скачать PDF (257 КБ)
Жогаль С.П., Жогаль С.И., Кулыба А.И. Исследование осциллятора ван дер Поля с запаздывающим отражением от нагрузки при различных типах случайных воздействий
Исследованы одночастотные колебания в автоколебательной системе ван дер Поля с запаздываниями в цепи обратной связи и от отраженной нагрузки при одновременных аддитивных и мультипликативных случайных воздействиях.
Ключевые слова: стохастические дифференциальные уравнения, одночастотные колебания, запаздывание, осциллятор ван дер Поля, аддитивных случайные воздействия, мультипликативные случайные воздействия.
Жогаль Сергей Петрович – кандидат физ.-мат. наук, доцент, декан факультета математики и технологий программирования Гомельского государственного университета им. Ф. Скорины
Жогаль Светлана Ивановна – кандидат технических наук, доцент кафедры математических проблем управления и информатики Гомельского государственного университета им. Ф. Скорины
А.И. Кулыба – Гомельский государственный университет им. Ф. Скорины
Скачать PDF (227 КБ)
Лубочкин А.В. Осуществление заданных движений динамических систем ограниченными оптимальными управлениями линейно-квадратичных задач
В классе ограниченных управлений рассматривается задача осуществления заданных движений динамическими системами. Методами оптимального управления строится алгоритм работы регулятора, который в режиме реального времени вычисляет (генерирует) текущие значения ограниченных обратных связей, с помощью которых замкнутая система устойчиво осуществляет заданное движение. Для решения этой задачи предлагается использовать реализацию оптимальной обратной связи линейно-квадратичных задач с ограничениями. Результаты иллюстрируются на задаче синтеза динамических систем, осуществляющих предельные циклы.
Ключевые слова: динамическая система, задача осуществления заданных движений, ограниченная стабилизирующая обратная связь, вспомогательная задача оптимального управления, регулятор.
Лубочкин Александр Васильевич – кандидат физ.-мат. наук, доцент Гомельского государст-венного университета им. Ф. Скорины
Скачать PDF (310 КБ)
Мегралиев Я.Т., Ализаде У.С. О задаче идентификации линейного источника для гиперболичеcкого уравнения третьего порядка с интегральным условием
Исследована задача идентификации линейного источника для одного уравнения третьего порядка, описывающего распространение продольных волн в диспергирующей среде с интегральным условием первого рода. Сначала исходная задача сводится к эквивалентной в определенном смысле задаче. С помощью метода Фурье эквивалентная задача сводится к решению системы интегральных уравнений. С помощью метода сжатых отображений доказываются существование и единственность решения системы интегральных уравнений, которая также является единственным решением эквивалентной задачи. Пользуясь эквивалентностью, доказывается существование и единственность классического решения исходной задачи.
Ключевые слова: обратная задача, уравнения третьего порядка, метод Фурье, классическое решение.
Мегралиев Яшар Топуш оглы – доктор физ.-мат. наук, профессор, зав. кафедрой дифференциальных и интегральных уравнений Бакинского государственного университета
Ализаде Улви Сафа оглы – аспирант кафедры дифференциальных и интегральных уравнений Бакинского государственного университета
Скачать PDF (315 КБ)
Монахов В.С., Трофимук А.А., Зубей Е.В. Конечные группы с ограничениями на две максимальные подгруппы
Подгруппа A называется полунормальной в группе G, если существует подгруппа B такая, что G=AB и AB1 – собственная в G подгруппа для каждой собственной подгруппы B1 из B. Если подгруппа A либо субнормальна в G, либо полунормальна в G, то A называется полусубнормальной в группе G. В настоящей работе доказана сверхразрешимость группы G при условии, что все силовские подгруппы из двух несопряженных максимальных подгрупп полусубнормальны в группе G. Установлена нильпотентность второго коммутанта (G')' группы G при условии, что все максимальные подгруппы из двух несопряженных максимальных подгрупп полусубнормальны в группе G.
Ключевые слова: сверхразрешимая группа, полусубнормальная подгруппа, коммутант, силовская подгруппа, максимальная подгруппа.
Монахов Виктор Степанович – доктор физ.-мат. наук, профессор Гомельского государственного университета им. Ф. Скорины
Трофимук Александр Александрович – кандидат физ.-мат. наук, докторант Гомельского государственного университета им. Ф. Скорины
Зубей Екатерина Владимировна – аспирант Гомельского государственного университета им. Ф. Скорины
Скачать PDF (285 КБ)
Мурашко В.И. Обобщенно ранговые композиционные формации конечных групп
Старовойтов А.П., Рябченко Н.В., Драпеза А.А. О существовании и единственности многочленов Эрмита – Паде первого рода
В работе введены новые понятия: вполненормальный индекс и вполнесовершенная система функций. С помощью этих понятий сформулирован и доказан критерий единственности, получены явные детерминантные представления многочленов Эрмита – Паде 1-го рода для произвольной системы степенных рядов. Полученные результаты дополняют и обобщают хорошо известные результаты в теории аппроксимаций Эрмита – Паде.
Ключевые слова: многочлены Эрмита – Паде, нормальный индекс, совершенная система, определитель Адамара, определитель Ганкеля.
Старовойтов Александр Павлович – доктор физ.-мат. наук, профессор Гомельского государственного университета им. Ф. Скорины
Рябченко Наталья Валерьевна – аспирант кафедры математического анализа и дифференциальных уравнений Гомельского государственного университета им. Ф. Скорины
Драпеза А.А. – магистрант кафедры математического анализа и дифференциальных уравнений Гомельского государственного университета им. Ф. Скорины
Скачать PDF (252 КБ)
Тютянов В.Н. Простые неабелевы группы с пронормальными вторыми максимальными подгруппами
В.И. Зенков поставил в Коуровскую тетрадь проблему 19.109: верно ли, что в конечной простой неабелевой группе G все максимальные подгруппы холловы тогда и только тогда, когда любая вторая максимальная подгруппа группы G является пронормальной в G? В настоящей работе показано, что данная проблема решается отрицательно.
Ключевые слова: конечная группа, вторая максимальная подгруппа, пронормальная подгруппа.
Тютянов Валентин Николаевич – доктор физ.-мат. наук, профессор Гомельского филиала Международного университета МИТСО
Скачать PDF (248 КБ)
Ху Б., Хуан Ц., Скиба А.Н. Конечные группы с заданными локальными секциями
Группа называется примарной, если она является конечной p-группой для некоторого простого числа p. Если
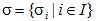 – некоторое разбиение множества 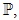 т. е.
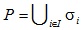 и 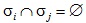 для всех 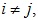 то мы говорим, что конечная группа G является: 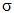 -примарной, если она является
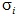 -группой для некоторого i;
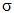 -нильпотентной, если 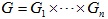 для некоторых
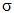 -примарных групп 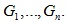
Если 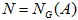 для некоторой примарной неединичной подгруппы A из G, то мы говорим, что
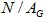 – локальная секция группы G. В данной работе изучается конечная группа G при условии, что все собственные локальные секции из G принадлежат насыщенной наследственной формации
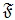 также устанавливается нормальная структура G в случае, когда все локальные секции из G являются 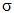 -нильпотентными.
Ключевые слова: конечная группа, наследственная насыщенная формация, 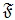 -гиперцентр, локальная секция, -гиперцентр, локальная секция, 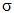 -нильпотентная группа. -нильпотентная группа.
Б. Ху – Цзянсунский педагогический университет, Сюйчжоу
Ц. Хуан – Цзянсунский педагогический университет, Сюйчжоу
Скиба Александр Николаевич – доктор физ.-мат. наук, профессор Гомельского государственного университета им. Ф. Скорины
Скачать PDF (269 КБ)
ИНФОРМАТИКА
Глубоков А.В., Жадан М.И., Березовская Е.М. Web-сервис автоматизированного проектирования и расчета фундаментов
Статья посвящена автоматизированному проектированию и расчету различных типов фундаментов мелкого заложения. Учитывается изменение под нагрузкой физико-механических характеристик грунтов оснований. Созданное приложение позволяет производить расчеты согласно нормам и правилам СНиП. Для написания web-сервиса использованы фреймворк Spring и архитектурный стиль программирования REST. Взаимодействие пользователя с web-сервисом реализовано через клиентское приложение на основе технологии JavaFX.
Ключевые слова: фундамент, грунт, слои, уровни, здания и сооружения, нагрузки, диагностика, отчет, проектирование.
Глубоков Андрей Владимирович – магистрант Гомельского государственного университета им. Ф. Скорины
Жадан Михаил Иванович – кандидат физ.-мат. наук, доцент кафедры вычислительной математики и программирования Гомельского государственного университета им. Ф. Скорины
Березовская Елена Михайловна – кандидат физ.-мат. наук, доцент кафедры вычислительной математики и программирования Гомельского государственного университета им. Ф. Скорины
Скачать PDF (676 КБ)
Таранчук В.Б. Средства и примеры интеллектуальной обработки данных для геологических моделей
Обсуждаются вопросы разработки, инструментального наполнения, использования интегрированного программного комплекса составителя цифровых геологических моделей. Отмечены возможности интерактивной графической визуализации и сравнения результатов. Представлены и обсуждаются результаты применения искусственных нейронных сетей в анализе и интерпретации геопространственных данных.
Ключевые слова: цифровая геологическая модель, система компьютерной алгебры Mathematica, интерактивная графическая визуализация, искусственные нейронные сети.
Таранчук Валерий Борисович – профессор кафедры компьютерных технологий и систем, факультет прикладной математики и информатики, Белорусский государственный университет
Скачать PDF (1,15 MБ)
|












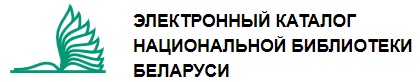
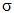 -субнормальных подгрупп конечной группы
-субнормальных подгрупп конечной группы
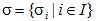 – некоторое разбиение множества всех простых чисел. В работе исследуется проблема перестановочности
– некоторое разбиение множества всех простых чисел. В работе исследуется проблема перестановочности 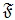 -групп, с-сверхразрешимых групп и ранговые формации. Описана структура групп из введенных формаций. В качестве частных случаев получен ряд результатов различных авторов. Также для предложенных формаций исследован вопрос Л.А. Шеметкова о пересечении
-групп, с-сверхразрешимых групп и ранговые формации. Описана структура групп из введенных формаций. В качестве частных случаев получен ряд результатов различных авторов. Также для предложенных формаций исследован вопрос Л.А. Шеметкова о пересечении
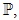 т. е.
т. е.
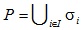 и
и 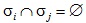 для всех
для всех 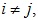 то мы говорим, что конечная группа G является:
то мы говорим, что конечная группа G является: 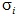 -группой для некоторого i;
-группой для некоторого i;
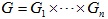 для некоторых
для некоторых
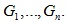 Если
Если 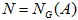 для некоторой примарной неединичной подгруппы A из G, то мы говорим, что
для некоторой примарной неединичной подгруппы A из G, то мы говорим, что
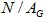 – локальная секция группы G. В данной работе изучается конечная группа G при условии, что все собственные локальные секции из G принадлежат насыщенной наследственной формации
– локальная секция группы G. В данной работе изучается конечная группа G при условии, что все собственные локальные секции из G принадлежат насыщенной наследственной формации