|
|
ПРОБЛЕМЫ ФИЗИКИ, МАТЕМАТИКИ И ТЕХНИКИ №3 (12) 2012
ФИЗИКА
Белый В.Н., Краморева Л.И., Петрова Е.С., Хило Н.А., Савицкий А.И. Особенности распределения потоков энергии при распространении квазибездифракционных световых пучков в поглощающих средах
Рассмотрено взаимодействие квазибездифракционных световых пучков с полубесконечной поглощающей средой. Показано, что при наличии поглощения проявляются новые закономерности поведения потоков энергии поля и пространственного профиля тепловыделения, не характерные для плоских волн или гауссовых пучков. Обнаруженные особенности в сочетании со свойством подавленной дифракционной расходимости центральной зоны пучка и реконструкции его поперечного профиля представляют практический интерес для лазерных технологий и решения задач неразрушающего контроля и диагностики.
Ключевые слова: квазибездифракционный пучок, полубесконечная поглощающая среда, поток энергии, зона тепловыделения.
Белый Владимир Николаевич – доктор физико-математических наук, профессор, главный научный сотрудник Института физики им. Б.И. Степанова НАН Беларуси, Минск, Беларусь
Краморева Лариса Ивановна – кандидат физико-математических наук, доцент Гомельского государственного медицинского университета, Гомель, Беларусь
Петрова Елена Сергеевна – кандидат физико-математических наук, доцент Гомельского государственного технического уни-верситета им. П.О. Сухого, Гомель, Беларусь
Хило Николай Анатольевич – кандидат физико-математических наук, доцент, ведущий научный сотрудник Института физики им. Б.И. Степанова НАН Беларуси, Минск, Беларусь
Савицкий Александр Иванович – ассистент Гомельского государственного медицинского университета, Гомель, Беларусь
Скачать PDF (429 КБ)
Валько Н.Г., Гуртовой В.Г. Электрические свойства сплавов Co-Ni, электроосажденных при воздействии рентгеновского излучения
Изложены основные закономерности формирования электролитических пленок Co-Ni при воздействии рентгеновского излучения. Обнаружены зависимости электрических свойств от режимов осаждения и облучения. Рассмотрены причины изменения удельного электросопротивления у облучаемых в процессе электроосаждения пленок, обусловленные изменением морфологии поверхности, элементного состава, уменьшением пористости и увеличением скорости электроосаждения под действием рентгеновского излучения.
Ключевые слова: рентгеновское излучение, гальванические пленки Co-Ni, удельное электрическое сопротивление.
Валько Наталья Георгиевна – кандидат физико-математических наук, доцент кафедры общей физики Гродненского государственного университета им. Я. Купалы, Гродно, Беларусь
Гуртовой Виталлий Геннадьевич – младший научный сотрудник ГО «НПЦ НАН Беларуси по материаловедению», Минск, Беларусь
Скачать PDF (579 КБ)
Гиргель С.С. Поляризационные и энергетические свойства векторных параксиальных гауссовых световых пучков
Найдены и исследованы поляризация и плотность потока энергии электромагнитного поля для векторных параксиальных гауссовых световых пучков с однородной и неоднородной поляризацией различных видов. Описаны несколько новых типов векторных параксиальных гауссовых световых пучков, например, пучки со спиральной эллиптической поляризацией.
Ключевые слова: параксиальные пучки, векторные пучки, световые пучки, гауссовы пучки, поляризационные свойства, энергетические свойства, неоднородная поляризация.
Гиргель Сергей Сергеевич – доктор физико-математических наук, профессор кафедры оптики Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (347 КБ)
Есман А.К., Кулешов В.К., Зыков Г.Л., Залесский В.Б. Поглощающее покрытие в терагерцовой части спектра
Исследовано поглощение электромагнитного излучения в частотном диапазоне 35 55 ТГц многослойным покрытием, верхний слой которого содержит массив пирамид субмикронных размеров, расположенных в строго геометрическом порядке по двум взаимно перпендикулярным направлениям. Показано, что предложенная структура обеспечивает по-тери на отражение -39,5 дБ на резонансной частоте 42,3 ТГц и позволяет получить изменение температуры чувствительного слоя 3 мК при плотности мощности входного излучения, равной 0,1 Вт/м2.
Ключевые слова: поглощающая структура, многослойное покрытие, массив пирамид, термочувствительность.
Есман Александр Константинович – доктор физико-математических наук, главный научный сотрудник лаборатории фотоэлектрических преобразователей Института физики имени Б.И. Степанова Национальной академии наук Беларуси, Минск, Беларусь
Кулешов Владимир Константинович – кандидат технических наук, ведущий научный сотрудник лаборатории фотоэлектрических преобразователей Института физики имени Б.И. Степанова Национальной академии наук Беларуси, Минск, Беларусь
Зыков Григорий Люцианович – кандидат физико-математических наук, старший научный сотрудник лаборатории фотоэлектрических преобразователей Института физики имени Б.И. Степанова Национальной академии наук Беларуси, Минск, Беларусь
Залесский Валерий Борисович – кандидат технических наук, заведующий лабораторией фотоэлектрических преобразователей Института физики имени Б.И. Степанова Национальной академии наук Беларуси, Минск, Беларусь
Скачать PDF (319 КБ)
Зажогин А.П., Умрейко Д.С., Зажогин А.А., Комяк А.И., Умрейко С.Д. Спектрально-структурные и фотокаталитические свойства водно-ацетоновых растворов нитрата и перхлората уранила
Изучены спектры люминесценции и поглощения растворов уранилнитрата и перхлората в воде, ацетоне и ацетонитриле. По положению коротковолновой полосы, соответствующей чисто электронному переходу, установлено различие образующихся структур. Дано возможное объяснение происходящим при этом процессам. Дополнительно обнаружена полимеризация ацетона, катализатором которой являются возбуждённые ионы уранила UO22+
Ключевые слова: спектры люминесценции и поглощения, структура, уранилнитрат, уранилперхлорат, ацетон, фотохимия.
Зажогин Анатолий Павлович – доктор физико-математических наук, профессор, профессор кафедры лазерной физики и спектроскопии Белорусского государственного университета, Минск, Беларусь
Умрейко Дмитрий Степанович – доктор физико-математических наук, профессор, главный научный сотрудник НИУ «Институт прикладных физических проблем им. А.Н. Севченко» Белорусского государственного университета, Минск, Беларусь
Комяк Анатолий Иванович – доктор физико-математических наук, профессор, профессор кафедры лазерной физики и спектроскопии Белорусского государственного университета, Минск, Беларусь
Зажогин Александр Анатольевич – кандидат физико-математических наук, старший научный сотрудник кафедры лазерной физики и спектроскопии Белорусского государственного университета, Минск, Беларусь
Умрейко Сергей Дмитриевич – старший научный сотрудник НИУ «Институт прикладных физических проблем им. А.Н. Севченко» Белорусского государственного университета, Минск, Беларусь
Скачать PDF (651 КБ)
Пилипцов Д.Г., Рогачев А.В., Федосенко Н.Н., Руденков А.С. Морфология и механические свойства углеродных покрытий, полученных из плазмы импульсного катодно-дугового разряда сложной формы
Предложен вакуумно-плазменный метод формирования углеродных покрытий, основанный на использовании при генерации углеродной плазмы катодно-дугового разряда с заданной формой импульса. Определен характер влияния параметров разряда на скорость роста покрытий, их морфологию.
Ключевые слова: углеродные покрытия, импульсный катодно-дуговой разряд, морфология, скорость роста.
Пилипцов Дмитрий Геннадьевич – ассистент кафедры оптики, научный сотрудник НИС Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Рогачев Александр Владимирович – член-корреспондент НАН Беларуси, доктор химических наук, профессор, ректор Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Федосенко Николай Николаевич – кандидат технических наук, доцент кафедры оптики, ведущий научный сотрудник НИС Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Руденков Александр Сергеевич – аспирант кафедры радиофизики и электроники, младший научный сотрудник НИСа Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (772 КБ)
Сердюков А.Н., Шалупаев С.В., Никитюк Ю.В., Середа А.А. Исследование процесса лазерного раскалывания кремниевых пластин, вырезанных в плоскости (110)
Представлены результаты моделирования процесса лазерного термораскалывания монокристаллического кремния. Расчет термоупругих полей, формируемых в кремниевой пластине в результате последовательного лазерного нагрева и воздействия хладагента, осуществлялся для среза (110) в трех различных вариантах перемещений лазерного пучка, а именно в направлениях [1–10], [001], [1–11].
Ключевые слова: трещина, лазерное раскалывание, кремниевая пластина.
Сердюков Анатолий Николаевич – доктор физико-математических наук, член-корреспондент НАН Беларуси, профессор кафедры оптики Гомельского государственного университета им. Ф.Скорины, Гомель, Беларусь
Шалупаев Сергей Викентьевич – кандидат физико-математических наук, доцент кафедры общей физики Гомельского государственного университета им. Ф.Скорины, Гомель, Беларусь
Никитюк Юрий Валерьевич – кандидат физико-математических наук, декан физического факультета Гомельского государственного университета им. Ф.Скорины, Гомель, Беларусь
Середа Андрей Александрович – ассистент кафедры радиофизики и электроники Гомельского государственного университета им. Ф.Скорины, Гомель, Беларусь
Скачать PDF (402 КБ)
МАТЕМАТИКА
Адарченко Н.М. О максимальных подгруппах конечных групп
В 1986 году В.А. Ведерников доказал, что если M – не нормальная максимальная подгруппа конечной разрешимой группы G, то M содержит нормализатор некоторой силовской подгруппы группы G. В статье доказано следующее обобщение теоремы В.А. Ведерникова.
Теорема. Пусть G – 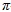 -разрешимая конечная группа. Пусть M – такая не нормальная максимальная подгруппа группы G, что | G : M | – степень простого числа p из -разрешимая конечная группа. Пусть M – такая не нормальная максимальная подгруппа группы G, что | G : M | – степень простого числа p из 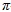 . Пусть H – некоторая холлова подгруппа из M такая, что p не делит | H |, причем либо . Пусть H – некоторая холлова подгруппа из M такая, что p не делит | H |, причем либо 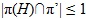 , либо | M : H | – , либо | M : H | – 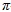 -число. Если ядро подгруппы -число. Если ядро подгруппы 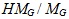 в в 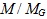 не равно 1, то не равно 1, то 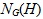 содержится в M. содержится в M.
Здесь 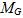 – ядро M в G, т. е. наибольшая нормальная подгруппа из G, содержащаяся в M ; – ядро M в G, т. е. наибольшая нормальная подгруппа из G, содержащаяся в M ; 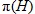 – множество всех простых делителей | H |. – множество всех простых делителей | H |.
Ключевые слова: 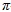 -разрешимая группа, максимальная подгруппа. -разрешимая группа, максимальная подгруппа.
Адарченко Никита Михайлович – студент математического факультета Гомельского государственного университета им. Ф.Скорины, Гомель, Беларусь
Скачать PDF (275 КБ)
Ахматова А.А. Спектральные свойства операторов взвешенного сдвига, порожденных линейными отображениями с условием Перрона
Витько Е.А. О строении наименьшего элемента секции Локетта 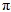 -разрешимого фиттингова функтора -разрешимого фиттингова функтора
Дашкова О.Ю. Локально разрешимые AFN-группы
В работе изучается RG-модуль A, такой, что R – коммутативное нетерово кольцо с единицей, G – локально разрешимая группа, 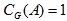 и любая собственная подгруппа H группы G, для которой фактор-модуль и любая собственная подгруппа H группы G, для которой фактор-модуль 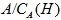 не является нетеровым R-модулем, конечно порождена. Доказано, что локально разрешимая группа G, удовлетворяющая заданным условиям, гиперабелева. Описана структура рассматриваемой группы G в случае, когда G – конечно порожденная разрешимая группа и фактор-модуль не является нетеровым R-модулем, конечно порождена. Доказано, что локально разрешимая группа G, удовлетворяющая заданным условиям, гиперабелева. Описана структура рассматриваемой группы G в случае, когда G – конечно порожденная разрешимая группа и фактор-модуль 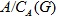 не является нетеровым R-модулем. не является нетеровым R-модулем.
Ключевые слова: групповое кольцо, локально разрешимая группа, нетеров R-модуль.
Дашкова Ольга Юрьевна – доктор физико-математических наук, доцент, профессор кафедры геометрии и алгебры Днепропетровского национального университета имени Олеся Гончара, Днепропетровск, Украина
Скачать PDF (383 КБ)
Заренок М.А. Сходимость рядов Фурье дифференцируемых функций многомерного p-адического аргумента
В данной статье рассматривается сходимость рядов Фурье функций многомерного р-адического аргумента. Даны определения многомерной функции Малера и частичных сумм ряда Фурье функций многомерного р-адического аргумента. Для получения основного результата был доказан ряд вспомогательных теорем: вычислена норма m -ой производной одномерной и многомерной функций Малера, получен критерий принадлежности функции пространству m раз непрерывно-дифференцируемых функций 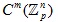 в терминах коэффициентов Малера. Доказана лемма о представлении коэффициентов и частичных сумм кратного ряда Фурье через коэффициенты и частичные суммы одномерного ряда. На основании данных результатов доказана теорема о том, что если в терминах коэффициентов Малера. Доказана лемма о представлении коэффициентов и частичных сумм кратного ряда Фурье через коэффициенты и частичные суммы одномерного ряда. На основании данных результатов доказана теорема о том, что если 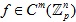 , тогда ряд Фурье функции сходится равномерно, если , тогда ряд Фурье функции сходится равномерно, если 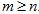 . Приведен пример функции . Приведен пример функции 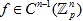 с расходящимся рядом Фурье. с расходящимся рядом Фурье.
Ключевые слова: функция р-адического векторного аргумента, ряд Фурье, коэффициенты Фурье, функция Малера
Заренок Максим Александрович – аспирант кафедры функционального анализа механико-математического факультета Белорусского государственного университета, Минск, Беларусь
Скачать PDF (405 КБ)
Ковалева В.А., Чжао Сяоюй. Конечные группы с заданными системами квазиперестановочных подгрупп
Пусть G – конечная группа. Подгруппа A группы G называется квазиперестановочной в G, если A либо покрывает, либо изолирует каждую максимальную пару (K,H) из G. Изучаются конечные группы с заданными системами квазиперестановочных подгрупп.
Ключевые слова: конечная группа, максимальная пара, (слабо) квазиперестановочная подгруппа, обобщенная подгруппа Фиттинга, p -нильпотентная группа, 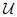 -гиперцентр. -гиперцентр.
Ковалева Виктория Александровна – магистрант математического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Чжао Сяоюй – магистрант математического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (313 КБ)
Косенок Н.С. Конечные группы с заданными обобщенно примитивными подгруппами
Найден новый критерий сверхразрешимости конечных групп.
Ключевые слова: примитивные подгруппы, конечная группа, разрешимая группа, сверхразрешимая группа, субнормально примитивная подгруппа, нормально примитивная подгруппа.
Косенок Николай Сергеевич – кандидат физико-математических наук, доцент кафедры математики и информационных технологий Гомельского филиала Международного института трудовых и социальных отношений, Гомель, Беларусь
Скачать PDF (320 КБ)
Кузьменков Д.С. Распараллеливание вычислений при решении задачи оптимального управления тепловым процессом в стержне
В статье рассматривается задача оптимального управления тепловым процессом в стержне с теплообменом на правом конце, которая сводится к задаче оптимального управления специальной системой обыкновенных дифференциальных уравнений большой размерности. Последняя решается методом квазидекомпозиции. Описывается алгоритм работы оптимального регулятора, формирующего в режиме реального времени текущие значения оптимальной обратной связи. Приводится численный пример, иллюстрирующий работу метода квазидекомпозиции.
Ключевые слова: тепловой процесс, задача оптимального управления, метод квазидекомпозиции, оптимальная обратная связь, оптимальный регулятор.
Кузьменков Дмитрий Сергеевич – кандидат физико-математических наук, доцент кафедры вычислительной математики и программирования Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (393 КБ)
Полевиков В.К., Волотовская Ю.Н. Численное моделирование равновесных капиллярных поверхностей с нерегулярными граничными условиями
Предлагается алгоритм численного моделирования равновесных капиллярных поверхностей с нерегулярными условиями контакта. Он представляет собой комбинацию итерационно-разностного метода решения краевой задачи и метода Рунге-Кутты решения начальной задачи для моделирования равновесных форм капиллярной поверхности, опирающейся на линию излома твердой стенки. Алгоритм апробирован на известной задаче капиллярной гидростатики о жидкости, вытекающей из капилляра.
Ключевые слова: капиллярная поверхность, параметрические дифференциальные уравнения, нерегулярные граничные условия, численное моделирование, вычислительный алгоритм, численные результаты.
Полевиков Виктор Кузьмич – кандидат физико-математических наук, доцент кафедры вычислительной математики факультета прикладной математики и информатики Белорусского государственного университета, Минск, Беларусь
Волотовская Юлия Николаевна – магистр технических наук, аспирантка кафедры вычислительной математики факультета прикладной математики и информатики Белорусского государственного университета, Минск, Беларусь
Скачать PDF (427 КБ)
Тютянов В.Н., Тютянова В.А. Критерий непростоты конечных факторизуемых групп
При изучении конечных факторизуемых групп для описания строения группы накладываются ограничения на строение сомножителей. Это мотивируется стремлением описать строение группы, сводя его к строению сомножителей либо получению некоторой информации о строении группы в зависимости от строения сомножителей. Классическими примерами являются теорема Ито о двуступенной разрешимости конечной группы, факторизуемой абелевыми подгруппами, и теорема Кегеля-Виландта о разрешимости конечной группы, представимой в виде произведения двух нильпотентных подгрупп. Отметим также гипотезу С.А. Чунихина о непрототе конечной группы, факторизуемой подгруппами с нетривиальными центрами, справедливость которой установил Л.С. Казарин.
Ключевые слова: конечная группа, простая неабелева группа, факторизуемая группа.
Тютянов Валентин Николаевич – доктор физико-математических наук, профессор кафедры высшей математики Международного института трудовых и социальных отношений, Гомель, Беларусь
Тютянова Валентина Анатольевна – старший преподаватель кафедры математики и информационных технологий Международного института трудовых и социальных отношений, Гомель, Беларусь
Скачать PDF (298 КБ)
ИНФОРМАТИКА
Смородин В.С. Анализ функционирования технологических процессов при наличии элементов потенциальной опасности
Предложена методика анализа надёжности функционирования вероятностных производственных систем, позволяющая определить параметры выполнения технологических операций, обеспечивающие заданный уровень надёжности функционирования технологического цикла. Практическая значимость состоит в реализации процедуры оценки вероятностных значений параметров надёжности функционирования компонентов производственной системы, обеспечивающей оптимальные варианты реализации структуры технологического цикла в рамках заданного критерия качества оценки выполнения технологического цикла.
Ключевые слова: анализ надежности, пространство состояний, оценка значений параметров, структура технологического цикла.
Смородин Виктор Сергеевич – доктор технических наук, зав. кафедрой математических проблем управления Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (332 КБ)
ТЕХНИКА
Врублевский И.А., Дик С.К., Терех А.С., Смирнов А.В., Чернякова К.В. Структура пленок пористого оксида алюминия, формируемых в электролитах на основе органических кислот
Рассмотрены закономерности анодного роста пленок пористого оксида алюминия в электролитах на основе водных растворов щавелевой и малоновой кислот. Показано, что при анодировании алюминия в гальваностатическом режиме в 0,3 М растворе щавелевой кислоты и в 0,8 M растворе малоновой кислоты формируются пористые пленки оксида алюминия с регулярно-упакованной ячеистой структурой. Анодирование алюминия в этих электролитах приводит к формированию пористых пленок с межпористым расстоянием в диапазоне 90–270 нм.
Ключевые слова: оксид алюминия, щавелевая кислота, малоновая кислота, пористая пленка.
Врублевский Игорь Альфонсович – кандидат технических наук, ведущий научный сотрудник НИЧ Белорусского государственного университета информатики и радиоэлектроники», Минск, Беларусь
Дик Сергей Константинович – кандидат физико-математических наук, доцент, декан факультета компьютерного проектирования Белорусского государственного университета информатики и радиоэлектроники», Минск, Беларусь
Терех Александр Сергеевич – ассистент кафедры ЭТТ Белорусского государственного университета информатики и радиоэлектроники», Минск, Беларусь
Смирнов Александр Владимирович – инженер кафедры ЭТТ Белорусского государственного университета информатики и радиоэлектроники», Минск, Беларусь
Чернякова Катерина Викторовна – ассистент кафедры химии Белорусского государственного университета информатики и радиоэлектроники», Минск, Беларусь
Скачать PDF (884 КБ)
|












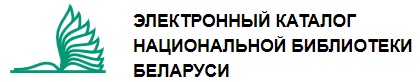
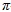 -разрешимая конечная группа. Пусть
-разрешимая конечная группа. Пусть 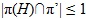 , либо |
, либо |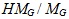 в
в 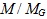 не равно 1, то
не равно 1, то 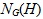 содержится в
содержится в 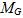 – ядро
– ядро 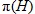 – множество всех простых делителей |
– множество всех простых делителей | 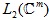 порожденный линейным отображением
порожденный линейным отображением 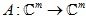 . Описаны свойства оператора
. Описаны свойства оператора 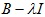 для
для 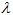 из спектра
из спектра 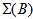 В частности, получено необходимое и достаточное условие, при котором оператор
В частности, получено необходимое и достаточное условие, при котором оператор 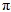 -разрешимого фиттингова функтора
-разрешимого фиттингова функтора
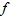 – сопряженный
– сопряженный 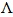 -нормально вложенный
-нормально вложенный 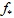 – наименьший по сильному вложению элемент секции Локетта функтора
– наименьший по сильному вложению элемент секции Локетта функтора 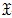 -функтор.
-функтор.
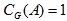 и любая собственная подгруппа
и любая собственная подгруппа 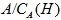 не является нетеровым R-модулем, конечно порождена. Доказано, что локально разрешимая группа
не является нетеровым R-модулем, конечно порождена. Доказано, что локально разрешимая группа 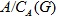 не является нетеровым R-модулем.
не является нетеровым R-модулем.
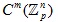 в терминах коэффициентов Малера. Доказана лемма о представлении коэффициентов и частичных сумм кратного ряда Фурье через коэффициенты и частичные суммы одномерного ряда. На основании данных результатов доказана теорема о том, что если
в терминах коэффициентов Малера. Доказана лемма о представлении коэффициентов и частичных сумм кратного ряда Фурье через коэффициенты и частичные суммы одномерного ряда. На основании данных результатов доказана теорема о том, что если 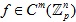 , тогда ряд Фурье функции сходится равномерно, если
, тогда ряд Фурье функции сходится равномерно, если 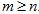 . Приведен пример функции
. Приведен пример функции 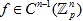 с расходящимся рядом Фурье.
с расходящимся рядом Фурье.
 -гиперцентр.
-гиперцентр.