|
|
ПРОБЛЕМЫ ФИЗИКИ, МАТЕМАТИКИ И ТЕХНИКИ №3 (8) 2011
ФИЗИКА
Андреев В.В., Бабич К.С. Квантовые и релятивистские эффекты для двухчастичных систем с корнельским потенциалом
Представлен новый метод численного решения уравнений на связанные состояния элементарных частиц в импульсном представлении с корнельским потенциалом. Получена квадратурная формула, которая может использоваться для решения как интегральных уравнений, так и для численного расчета интегралов. Исследованы некоторые эффекты для двухчастичных квантовых систем с корнельским потенциалом. Для случая нерелятивистского уравнения Шредингера с корнельским потенциалом исследовано поведение волновых функций вблизи критического значения параметра кулоновского потенциала, а также зависимость критического значения при изменении параметра запирающей части потенциала.
Ключевые слова: связанные состояния, импульсное представление, квадратурная формула, корнельский потенциал, коллапс, волновая функция, уравнение Шредингера.
Андреев Виктор Васильевич – кандидат физико-математических наук, доцент, заведующийкафедрой теоретической физики физического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Бабич Константин Сергеевич – ассистент кафедры теоретической физики физического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (411 КБ)
Васькевич В.В., Гайшун В.Е., Коваленко Д.Л., Сидский В.В. Защитные золь-гель покрытия с гидрофобными свойствами
В работе рассматривается возможность создания защитных SiO2 покрытий на основе золь-гель метода путем гидролиза металлоорганических соединений кремния в водно-спиртовой смеси. Исследуется реология приготовленных пленкообразующих растворов в зависимости от времени и условий хранения раствора. Описаны оптимальные параметры нанесения и термообработки для получения однородных покрытий. Исследуется механическая стойкость к истиранию как основной вид испытания покрытий на прочность и адгезию к поверхности подложки. Анализируются свойства гидрофобности полученных покрытий в зависимости от состава и температуры обработки.
Ключевые слова: золь-гель технология, реология, термообработка, защитные покрытия, гидрофобные свойства.
Васькевич Василий Васильевич – младший научный сотрудник научно-исследовательского сектора «Гомельский государственный университет», Гомель, Беларусь
Гайшун Владимир Евгеньевич – кандидат физико-математических наук, доцент кафедры оптики физического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Коваленко Дмитрий Леонидович – кандидат физико-математических наук, доцент, заместитель декана физического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Сидский Виталий Валерьевич – научный сотрудник научно-исследовательского сектора «Гомельский государственный университет», Гомель, Беларусь
Скачать PDF (378 КБ)
Гуделев В.Г., Кулак Г.В., Матвеева А.Г., Николаенко Т.В. Лазерное возбуждение
импульсов продольных и сдвиговых ультразвуковых волн в твердых телах в ближней зоне
Исследованы особенности оптико-акустического возбуждения акустических импульсов продольных и сдвиговых ультразвуковых волн в ближней зоне Френеля для дифракции на отверстии прямоугольной формы. Установлено некоторое увеличение амплитуды и уменьшение длительности акустического импульса при переходе из ближней зоны Френеля в дальнюю зону Фраунгофера. Показано, что при смещении от центра отверстия в зоне Френеля амплитуда акустического импульса уменьшается и длительность увеличивается; при переходе в область геометрической тени амплитуда импульса значительно уменьшается.
Ключевые слова: лазерное возбуждение, ультразвуковая волна, длительность и амплитуда импульса, зона дифракции, твердое тело.
Гуделев Валерий Георгиевич – кандидат физико-математических наук, ведущий научный сотрудник Института физики им. Б.И. Степанова НАНБ, Минск, Беларусь
Кулак Геннадий Владимирович – доктор физико-математических наук, профессор кафедры общей физики и МПФ Мозырского государственного педагогического университета им. И.П. Шамякина, Мозырь, Беларусь
Матвеева Алина Григорьевна – аспирантка кафедры общей физики и МПФ Мозырского государственного педагогического университета им. И.П. Шамякина, Мозырь, Беларусь
Николаенко Татьяна Викторовна – кандидат физико-математических наук, старший преподаватель кафедры общей физики и МПФ Мозырского государственного педагогического университета им. И.П. Шамякина, Мозырь, Беларусь
Скачать PDF (317 КБ)
Малютина-Бронская В.В., Поликанин А.М., Залесский В.Б., Семченко А.В., Сидский В.В., Гайшун В.Е. Получение гетероструктур SIO2/ZnO/Si золь-гель методом
В работе рассматривается анализ вольт-амперных, вольт-фарадных характеристик структур SiO2/ZnO/Si, полученных золь-гель методом с использованием различных исходных веществ, таких как нитрат цинка, хлорид цинка и ацетат цинка. Рассчитана плотность дефектов на границе раздела ZnO/Si с использованием Мотт–Шоттки зависимостей
С2(U). Определен основной механизм проводимости – токи, ограниченные пространственным зарядом. Показано, что пленки, полученные с использованием ацетата цинка, обладают фоточувствительностью.
Ключевые слова: золь-гель, ZnO,вольт-фарадные характеристики, вольт-амперные характеристики.
Малютина-Бронская Виктория Владимировна – младший научный сотруд-ник Лаборатории фотоэлектрических преобразователей Института физики им. Б.И. Степанова НАН Беларуси, Минск, Беларусь
Поликанин Александр Михайлович – кандидат химических наук, старший научный сотрудник Лаборатории фотоэлектрических преобразователей Института физики им. Б.И. Степанова НАН Беларуси, Минск, Беларусь
Залесский Валерий Борисович – кандидат технических наук, заведующий Ла-боратории фотоэлектрических преобразователей Института физики им. Б.И. Степанова НАН Беларуси, Минск, Беларусь
Семченко Алина Валентиновна – кандидат физико-математических наук, доцент кафедры радиофизики и электроники физического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Сидский Виталий Валерьевич – научный сотрудник научно-исследовательского сектора «Гомельский государственный университет», Гомель, Беларусь
Гайшун Владимир Евгеньевич – кандидат физико-математических наук, до-цент кафедры оптики физического факультета учреждения образования «Го-мельский государственный университет им. Ф. Скорины», Гомель, Беларусь
Скачать PDF (906 КБ)
Самофалов А.Л., Семченко И.В., Хахомов С.А. Моделирование и исследование искусственных анизотропных структур с большой киральностью в СВЧ диапазоне
В СВЧ диапазоне проведено моделирование киральных свойств образца искусственной среды, состоящей из медных спиралей. Сравнение рассчитанных значений угла поворота плоскости поляризации волны, прошедшей через искусственную структуру, с экспериментальными результатами позволило сделать вывод, что предложенная модель качественно описывает свойства искусственной структуры с большой киральностью в СВЧ диапазоне.
Ключевые слова: композитные среды, киральность, спиральный элемент, поворот плоскости поляризации.
Самофалов Андрей Леонидович – старший преподаватель кафедры общей физики физического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Семченко Игорь Валентинович – доктор физико-математических наук, профессор, проректор по учебной работе Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Хахомов Сергей Анатольевич – кандидат физико-математических наук, доцент, проректор по учебной работе Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (522 КБ)
Ярмоленко М.А., Рогачев А.А., Рогачев А.В., Горбачев Д.Л. Кинетические особенности диспергирования кремнийорганических соединений в вакууме и молекулярная структура покрытий, осажденных из летучих продуктов диспергирования
Показано, что особенности кинетики электронно-лучевого диспергирования кремнийорганических соединений и молекуляр-ной структуры слоев, осажденных из образовавшейся при диспергировании газовой фазы, обусловлены процессами химического взаимодействия, протекающими в зоне действия потока электронов на мишень. При диспергировании в условиях плазменной активации газовой фазы формируются слои, имеющие меньшую плотность углеводородных фрагментов и большую плотность ненасыщенных связей. Установлена возможность образования высокодисперсных композиционных покрытий на основе кремнийорганических соединений, молекулярная структура которых имеет заметные отличия от структуры исходных компонент.
Ключевые слова: кремнийорганическое соединение, электронно-лучевое диспергирование, морфология, молекулярная структура, композиционное покрытие.
Ярмоленко Максим Анатольевич – кандидат технических наук, доцент кафедры радиофизики и электроники Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Рогачев Александр Александрович – кандидат технических наук, старший научный сотрудник НИСа Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Рогачев Александр Владимирович – член-корреспондент НАН Беларуси, доктор химических наук, профессор, ректор Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Горбачев Дмитрий Леонидович – младший научный сотрудник НИСа Гомельского государственно-го университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (1,11 МБ)
МАТЕМАТИКА
Андреева Д.П., Скиба А.Н. Конечные группы с заданными максимальными цепями длины 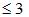
В работе получено описание конечной группы, у которой в каждой ее максимальной цепи длины три имеется собственная
S-квазинормальная подгруппа, а также описание конечной группы, у которой все ее 3-максимальные подгруппы субнормальны
(S-квазинормальны).
Ключевые слова: силовская подгруппа, группа Шмидта,
n-максимальная подгруппа, нильпотентная группа, максимальная цепь длины n,
разрешимая группа,
S-квазинормальная подгруппа, субнормальная подгруппа.
Андреева Дина Петровна – преподаватель-стажер кафедры алгебры и геометрии математического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скиба Александр Николаевич – доктор физико-математических наук, профессор кафедры алгебры и геометрии математического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (455 КБ)
Бедюк Н.В. Обобщенный стохастический интеграл по непрерывному мартингалу
В алгебре обобщенных случайных процессов рассматривается процесс, задаваемый стохастическим интегралом по непрерывному мартингалу. Найдены условия, при которых рассматриваемый обобщенный процесс ассоциирует обычный случайный процесс. Описан общий вид указанного случайного процесса.
Ключевые слова: алгебра обобщенных случайных процессов, мартингал, стохастический интеграл.
Бедюк Надежда Владимировна – аспирантка кафедры функционального анализа механико-математического факультета Белорусского государственного университета, Минск, Беларусь
Скачать PDF (395 КБ)
Дыба Р.В. Теорема Нехари на компактных абелевых группах с линейно упорядоченной группой характеров
Теорема Нехари для классических ганкелевых операторов обобщается на случай компактных абелевых групп с линейно упо-рядоченной группой характеров.
Ключевые слова: компактная абелева группа, линейно упорядоченная группа, оператор Ганкеля, пространство Харди.
Дыба Роман Викторович – математический факультет Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (320 КБ)
Жизневский П.А. Элементы высоты 3 решетки
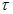 -замкнутых
n-кратно -замкнутых
n-кратно
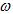 -композиционных формаций -композиционных формаций
Коржик Р.И., Жогаль C.П. Влияние запаздывания на стационарные состояния неавтономного осциллятора Ван-дер-Поля-Дуффинга
Исследовано влияние запаздывания на динамические режимы укороченного уравнения неавтономного осциллятора Ван-дер-Поля-Дуффинга с внешним гармоническим воздействием. Выведено укороченное уравнение и построены карты динамических режимов для различных значений параметра, характеризующего запаздывание.
Ключевые слова: осциллятор Ван-дер-Поля-Дуффинга, стационарные состояния, влияние запаздывания, укороченное уравнение, внешнее периодическое воздействие, критерий устойчивости Рауса-Гурвица, бифуркации.
Коржик Руслан Игоревич – аспирант кафедры математических проблем управления Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Жогаль Сергей Петрович – кандидат физико-математических наук, доцент, декан математического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (793 КБ)
Мартынов И.П., Парманчук О.Н., Пецевич В.М. Об одной перекрестной системе двух дифференциальных уравнений со свойством Пенлеве
В статье рассмотрена перекрестная система двух дифференциальных уравнений второй степени относительно производной и третьей степени относительно переменных. Найдены необходимые и достаточные условия наличия свойства Пенлеве у решений данной системы.
Ключевые слова: перекрестная система дифференциальных уравнений, свойство Пенлеве, особое решение, тест Пенлеве, резонансы.
Мартынов Иван Платонович – доктор физико-математических наук, профессор кафедры математического анализа и дифференциальных уравнений Гродненского государственного университета им. Я. Купалы, Гродно, Беларусь
Парманчук Ольга Николаевна – аспирант кафедры математического анализа и дифференциальных уравнений Гродненского государственного университета им. Я. Купалы, Гродно, Беларусь
Пецевич Виктор Михайлович – кандидат физико-математических наук, доцент кафедры математического анализа и дифференциальных уравнений Гродненского государственного университета им. Я. Купалы, Гродно, Беларусь
Скачать PDF (310 КБ)
Старовойтов А.Н. Система массового обслуживания с групповым поступлением, групповым обслуживанием и катастрофическими сбоями
Рассматривается однолинейная система массового обслуживания, в которую заявки поступают группами случайного размера. На обслуживание также выбирается группа случайного размера. Кроме того, в систему поступает поток катастрофических сбоев. Катастрофический сбой полностью очищает очередь системы, если она не пуста, и не оказывает никакого влияния, если очередь пуста. Находится стационарное распределение процесса, описывающего поведение данной системы.
Ключевые слова: система массового обслуживания, групповое поступление, групповое обслуживание, катастрофический сбой.
Старовойтов Александр Николаевич – кандидат физико-математических наук, доцент кафедры прикладной математики Белорусского государственного университета транспорта, Гомель, Беларусь
Скачать PDF (306 КБ)
Тавгень О.И., Ду Цзюньхуа, Лю Сщуньянь. Унипотентность образа представления группы
F2 при отображении примитивных элементов в унипотентные матрицы с малыми клетками Жордана
Доказано, что образ представления свободной группы
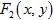 в в
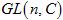 является унипотентной подгруппой, если является унипотентной подгруппой, если
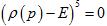 для любого примитивного элемента
p
и для любого примитивного элемента
p
и
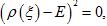
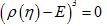 для каких-то ассоциированных примитивных элементов
для каких-то ассоциированных примитивных элементов
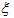 и и
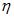 группы группы
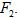
Ключевые слова: унипотентная подгруппа, примитивный элемент, представление группы.
Тавгень Олег Игнатьевич – доктор физико-математических наук, профессор, заведующий кафедрой высшей алгебры Белорусского государственного университета, Минск, Беларусь
Ду Цзюньхуа – доцент Института естественных наук Цицихарского университета, Цицикар, Китай
Лю Сщуньянь – магистр Харбинского научно-технического Университета, Харбин, Китай
Скачать PDF (292 КБ)
Царев А.А. О недистрибутивности решетки всех n-кратно
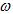 -композиционных формаций -композиционных формаций
Якубович О.В., Боярович Ю.С., Летунович Ю.Е., Ворошилов Д.Е. Применение сети Джексона к моделированию гарантийного обслуживания сельскохозяйственной техники
В работе рассматривается математическая модель процесса гарантийного обслуживания сельскохозяйственных машин, выпускаемых ПО «Гомсельмаш», региональными дилерскими центрами, функционирование каждого центра описано сетью массового обслуживания. Найдены стационарное распределение вероятностей состояний сети и условия эргодичности, получены формулы для определения числовых характеристик стационарного функционирования сети.
Ключевые слова: сеть массового обслуживания, стационарное распределение, условия эргодичности, числовые характеристики.
Якубович Оксана Владимировна – кандидат физико-математических наук, доцент кафедры экономической кибернетики и теории вероятностей Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Боярович Юлия Сигизмундовна – кандидат физико-математических наук, ассистент кафедры экономической кибернетики и теории вероятностей Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Летунович Юлия Евгеньевна – ассистент кафедры экономической кибернетики и теории вероятностей Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Ворошилов Дмитрий Евгеньевич – ведущий специалист конструкторско-исследовательского отдела экспертиз и управления качеством республиканского конструкторского унитарного предприятия «ГСКБ по зерноуборочной и кормоуборочной технике», Гомель, Беларусь
Скачать PDF (319 КБ)
ИНФОРМАТИКА
Ратобыльская Д.В. Выбор рационального варианта организации транспортной сети сообщения на основе вероятностно-алгебраического моделирования
Статья посвящена применению метода вероятностно-алгебраического моделирования для исследования вероятностных характеристик сложных систем. Содержит описание идеи метода и методологию вероятностно-алгебраического моделирования. В статье приведен пример описания модели транспортной сети и оценка организации сообщения средствами метода.
Ключевые слова: вероятностно-алгебраическая модель, моделирование, граф, транспортная сеть, сеть сообщения.
Ратобыльская Дарья Викторовна – аспирант кафедры математических проблем управления математического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (785 КБ)
Сукач Е.И. Подходы к снижению размерности многокомпонентных структурно-сложных систем со многими состояниями при оценке их надёжности
Описываются подходы для снижения размерности структурно-сложных систем при оценке их показателей надежности. Для участков системы с параллельно-последовательным соединением компонентов предлагается применение вероятностно-алгебраического моделирования. Расчёт надёжности структурно-сложных систем со многими состояниями обеспечивается применением методики сведения моделей систем со многими состояниями к расчетным бинарным моделям.
Ключевые слова: надёжность многокомпонентной системы, структурно-сложная система, системы со многими состояниями, вероятностно-алгебраическое моделирование, вероятностные показатели надёжности.
Сукач Елена Ивановна – кандидат технических наук, доцент кафедры математических проблем управления математического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (326 КБ)
Шилько С.В., Кузьминский Ю.Г., Борисенко М.В. Математическая модель и программная реализация мониторинга сердечно-сосудистой системы
Показаны возможности первичной диагностики сердечно-сосудистой системы на основе гидродинамической модели кровото-ка, реализованной в программном продукте BIODIS V2.2.
Ключевые слова: сердечно-сосудистая система, гемодинамика, давление, адаптивность, первичная диагностика, компьютерное моделирование, программное обеспечение.
Шилько Сергей Викторович – кандидат технических наук, доцент, заведующий отделом «Механика адаптивных материалов и биомеханика» Института механики металлополимерных систем им. В.А. Белого НАН Беларуси, Гомель, Беларусь
Кузьминский Юрий Гариевич – старший научный сотрудник Института механики металлополимерных систем им. В.А. Белого НАН Беларуси, Гомель, Беларусь
Борисенко Марина Владимировна – старший преподаватель кафедры ин-формационных технологий, аспирант кафедры прикладной математики Белорусский государственный университет транспорта, Гомель, Беларусь
Скачать PDF (647 КБ)
Якимов Е.А., Демиденко О.М., Албкеират Д.М. О восстановлении шумовой составляющей в последовательностях данных методом сингулярного спектрального анализа
Рассматриваются методика и результаты исследования последовательностей данных с равномерным, нормальным и экспоненциальным шумом путем преобразования методом сингулярного спектрального анализа (SSA-методом). Показываются особенности восстановления шумовой составляющей в последовательностях данных, предложен алгоритм корректировки восстановленной шумовой составляющей с учетом стандартного отклонения.
Ключевые слова: SSA-метод, временная последовательность данных; равномерное, нормальное, экспоненциальное распределение; коррекция.
Якимов Евгений Анатольевич – аспирант кафедры автоматизированных систем управления Белорусско-Российского университета, Могилев, Беларусь
Демиденко Олег Михайлович – доктор технических наук, профессор, проректор по научной работе Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Албкеират Джихад Мохаммад – аспирант кафедры автоматизированных сис-тем управления Белорусско-Российского университета, Могилев, Беларусь
Скачать PDF (406 КБ)
|












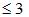
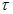 -замкнутых
-замкнутых
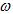 -композиционных формаций
-композиционных формаций
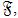 имеющей высоту 3 в решетке всех
имеющей высоту 3 в решетке всех
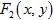 в
в
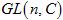 является унипотентной подгруппой, если
является унипотентной подгруппой, если
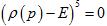 для любого примитивного элемента
для любого примитивного элемента
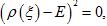
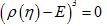 для каких-то ассоциированных примитивных элементов
для каких-то ассоциированных примитивных элементов
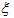 и
и
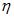 группы
группы
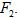
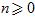 и
и