|
|
ПРОБЛЕМЫ ФИЗИКИ, МАТЕМАТИКИ И ТЕХНИКИ №1 (2) 2010
Гиргель С.С. Скалярные параксиальные двумерные гауссовоподобные световые пучки
Предложен унифицированный формализм, позволяющий вывести выражения для параксиальных двумерных гауссовоподобных световых пучков Куммера-Гаусса и Гельмгольца-Гаусса и установить взаимосвязи между ними. Сформулированы простые условия их физической реализуемости. Найдены новые типы пучков Куммера-Гаусса. Такие пучки описываются произведением гауссиана на функции Куммера комплексного аргумента и неотрицательного целочисленного индекса n.
Ключевые слова: параксиальные пучки, пучки Эрмита-Гаусса, пучки Куммера-Гаусса, пучки Гельмгольца-Гаусса, гауссовоподобные пучки.
Гиргель Сергей Сергеевич – доктор физико-математических наук, профессор кафедры оптики Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (348 KБ)
Егоров А.Н., Сердюков А.Н. Влияние поля тяготения на радиальное распространение электромагнитных волн в киральной среде нейтронной звезды
Построены материальные уравнения электродинамики киральной сплошной среды, находящейся в сильном гравитационном поле. Рассмотрено влияние тяготения на распространение электромагнитных волн в естественно гиротропной среде. Полученные решения для неоднородных электромагнитных волн позволяют моделировать процесс распространения электромагнитного излучения в материи нейтронных звезд.
Ключевые слова: гравитационное взаимодействие, электромагнитные волны.
Егоров Александр Николаевич – ассистент кафедры теоретической физики Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Сердюков Анатолий Николаевич – член-корреспондент НАН Беларуси, доктор физико-математических наук, профессор кафедры оптики Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (320 KБ)
МАТЕМАТИКА
Аниськов В.В. О неприводимых разрешимых локальных формациях p-разложимого дефекта
Рассматриваются только конечные группы. Пусть 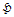 – некоторый класс групп, а – некоторый класс групп, а 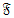 – некоторая локальная формация. Через – некоторая локальная формация. Через 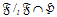 обозначим решетку всех локальных формаций, заключенных между обозначим решетку всех локальных формаций, заключенных между 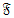 и и 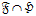 . Если такая решетка имеет конечную длину . Если такая решетка имеет конечную длину 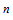 , то число , то число 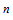 называется называется 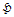 -дефектом формации -дефектом формации 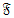 . Локальная формация . Локальная формация 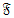 называется приводимой, если она может быть представлена в виде объединения своих собственных локальных подформаций. В данной работе получено полное описание неприводимых разрешимых локальных формаций конечных групп, имеющих p-разложимый дефект 3. называется приводимой, если она может быть представлена в виде объединения своих собственных локальных подформаций. В данной работе получено полное описание неприводимых разрешимых локальных формаций конечных групп, имеющих p-разложимый дефект 3.
Ключевые слова: конечная группа, класс групп, локальная формация, решетка, длина решетки, локальный экран, 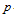 -разложимая группа, неприводимая локальная формация, разрешимая локальная формация. -разложимая группа, неприводимая локальная формация, разрешимая локальная формация.
Аниськов Валерий Валерьевич – доцент кафедры алгебры и геометрии Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (2,14 МБ)
Вареникова Е.В. Временные симметрии двумерных неавтономных дифференциальных систем
Отражающая функция В.И. Мироненко применена к исследованию периодических решений дифференциальных систем.
Ключевые слова: отражающая функция, дифференциальная система, периодическое решение, отображение за период.
Варенникова Елена Владимировна – ассистент кафедры математики, физики и информатики Брянского государственного университета им. И.Г. Петровского, Брянск, Россия
Скачать PDF (310 KБ)
Княгина В.Н. О 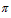 -разрешимости конечной группы с частично перестановочной -разрешимости конечной группы с частично перестановочной 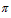 -холловой подгруппой -холловой подгруппой
Устанавливаются признаки 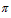 -разрешимости конечной группы при условии, что ее -разрешимости конечной группы при условии, что ее 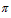 -холлова подгруппа перестановочна с некоторыми подгруппами всей группы. В частности, получена -холлова подгруппа перестановочна с некоторыми подгруппами всей группы. В частности, получена 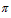 -разрешимость таких групп в двух случаях: -разрешимость таких групп в двух случаях: 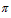 -холлова подгруппа 2-нильпотентна; -холлова подгруппа 2-нильпотентна; 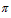 -холлова подгруппа разрешима и -холлова подгруппа разрешима и 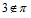 . Кроме того, устанавливается разрешимость конечной группы в случае, если 2-нильпотентная . Кроме того, устанавливается разрешимость конечной группы в случае, если 2-нильпотентная 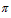 -холлова подгруппа группы имеет нечетный индекс. -холлова подгруппа группы имеет нечетный индекс.
Ключевые слова: конечная группа, полунормальная подгруппа, 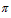 -холлова подгруппа, -холлова подгруппа, 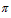 -разрешимая группа. -разрешимая группа.
Княгина Виктория Николаевна – кандидат физико-математических наук, доцент кафедры естественных наук Гомельского инженерного института Министерства по чрезвычайным ситуациям Республики Беларусь, Гомель, Беларусь
Скачать PDF (311 KБ)
Ковалева В.А., Скиба А.Н. О 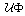 -гиперцентре конечных групп -гиперцентре конечных групп
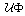 -гиперцентром группы -гиперцентром группы 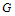 называют произведение всех нормальных подгрупп группы называют произведение всех нормальных подгрупп группы 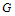 , у которых все их нефраттиньевы , у которых все их нефраттиньевы 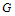 -главные факторы являются циклическими. Доказана следующая теорема. Теорема. Пусть -главные факторы являются циклическими. Доказана следующая теорема. Теорема. Пусть 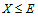 – разрешимые нормальные подгруппы группы – разрешимые нормальные подгруппы группы 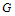 . Предположим, что каждая максимальная подгруппа каждой силовской подгруппы из X условно покрывает или изолирует каждую максимальную пару (M,G), где . Предположим, что каждая максимальная подгруппа каждой силовской подгруппы из X условно покрывает или изолирует каждую максимальную пару (M,G), где 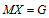 . Если . Если 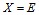 или или 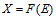 , то , то 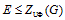 . .
Ключевые слова: 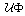 -гиперцентр, сверхразрешимая группа, максимальная пара, свойство (условного) покрытия и изолирования для подгрупп, -гиперцентр, сверхразрешимая группа, максимальная пара, свойство (условного) покрытия и изолирования для подгрупп, 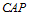 -подгруппа. -подгруппа.
Ковалева Виктория Александровна – студентка математического факультета Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (346 KБ)
Мироненко В.И. Временные симметрии уравнения Риккати
Теория отражающей функции применяется к изучению дифференциального уравнения Риккати.
Ключевые слова: дифференциальное уравнение, периодическое решение, отображение за период.
Мироненко Владимир Иванович – кандидат физико-математических наук, профессор, заведующий кафедрой дифференциальных уравнений Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (306 KБ)
Мисюк В.Р. Об обратной теореме теории рациональных приближений для пространств Бергмана
В работе исследуются обратные теоремы теории рациональных приближений. Доказаны аналоги таких теорем в пространстве Бергмана аналитических функций в круге.
Ключевые слова: рациональные функции, наилучшее рациональное приближение, пространство Бергмана, рациональная аппроксима-ция.
Мисюк Виктор Романович – кандидат физико-математических наук, доцент кафедры теории функций, функционального анализа и прикладной математики факультета математики и информатики Гродненского государственного университета им. Я. Купалы, Гродно, Беларусь
Скачать PDF (357 KБ)
ИНФОРМАТИКА
Левчук В.Д., Чечет П.Л. Способы интеграции имитационных моделей в информационную систему заказчика
Рассматриваются вопросы интеграции имитационных моделей в информационную среду заказчика. На примерах разработанных имитационных моделей рассмотрено использование различных контейнеров ввода/вывода и модулей преобразования форматов результатов моделирования.
Ключевые слова: модель, контейнеры, информационная среда, форматы обмена данными.
Левчук Виктор Дмитриевич – кандидат технических наук, доцент, заведующий кафедрой автоматизированных систем обработки информации Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Чечет Павел Леонидович – кандидат технических наук, ассистент кафедры математических проблем управления Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (4,87 МБ)
Маслович С.Ф. Транзактно-процессный подход к формализации имитационного моделирования распределенной обработки информации в сети многопроцессорной вычислительной системы
Описывается транзактно-процессный подход к формализации распределенной обработки информации в сети многопроцессорной вычислительной системы. Задача распределенной обработки представляется в виде сетевого графика. Динамика взаимодействия компонентов сети по использованию ресурсов ее узлов исследуется с помощью двух типов имитационных моделей: модель оборудования сети и модель рабочей нагрузки, имеющая вид сетевого графика.
Ключевые слова: имитационная модель, рабочая нагрузка, распределенная обработка информации, многопроцессорная вы-числительная система.
Маслович Сергей Федорович – ассистент кафедры математических проблем управления Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (402 KБ)
Смородин В.С., Гончаров А.Н., Клименко А.В., Жигарь А.В. Система контроля имитации технологических процессов с вероятностными параметрами их функционирования
Рассматривается новый подход к исследованию вероятностных технологических процессов с дискретным характером технологического цикла, в котором временные интервалы выполнения отдельных операций являются случайными величинами, а нарушение ритма производственного процесса может стать причиной серьезной аварийной ситуации. Изложен способ формализации вероятностного технологического процесса и имитация процессов управления технологическим циклом на основе новой версии агрегатной системы автоматизации имитационного моделирования.
Ключевые слова: вероятностный технологический процесс, система контроля, вероятностный сетевой график, имитационный эксперимент.
Смородин Виктор Сергеевич – доктор технических наук, доцент, и.о. заведующего кафедрой математических проблем управления Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Гончаров Александр Николаевич – аспирант кафедры математических проблем управления Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Клименко Андрей Валерьевич – ассистент кафедры математических проблем управления Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Жигарь Александр Викторович – магистрант кафедры математических проблем управления Гомельского государственного университета им. Ф. Скорины, Гомель, Беларусь
Скачать PDF (3,1 МБ)
|












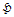 – некоторый класс групп, а
– некоторый класс групп, а 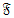 – некоторая локальная формация. Через
– некоторая локальная формация. Через 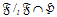 обозначим решетку всех локальных формаций, заключенных между
обозначим решетку всех локальных формаций, заключенных между 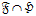 . Если такая решетка имеет конечную длину
. Если такая решетка имеет конечную длину 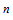 , то число
, то число 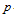 -разложимая группа, неприводимая локальная формация, разрешимая локальная формация.
-разложимая группа, неприводимая локальная формация, разрешимая локальная формация.
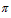 -разрешимости конечной группы с частично перестановочной
-разрешимости конечной группы с частично перестановочной 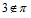 . Кроме того, устанавливается разрешимость конечной группы в случае, если 2-нильпотентная
. Кроме того, устанавливается разрешимость конечной группы в случае, если 2-нильпотентная 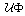 -гиперцентре конечных групп
-гиперцентре конечных групп
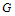 называют произведение всех нормальных подгрупп группы
называют произведение всех нормальных подгрупп группы 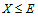 – разрешимые нормальные подгруппы группы
– разрешимые нормальные подгруппы группы 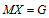 . Если
. Если 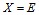 или
или 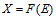 , то
, то 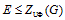 .
.
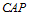 -подгруппа.
-подгруппа.